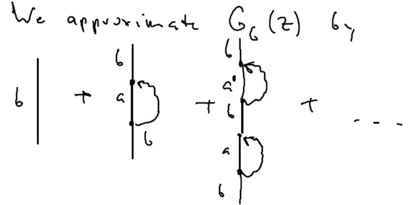Difference between revisions of "Resonant scattering"
imported>Ichuang |
imported>Ketterle |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<categorytree mode=pages style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;" hideprefix=auto>8.422</categorytree> | <categorytree mode=pages style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;" hideprefix=auto>8.422</categorytree> | ||
| − | There are several important reasons to consider resonant scattering. | + | There are several important reasons to consider resonant scattering. Resonant scattering is when we have the strongest scattering rate, and as a result, the most sensitive fluorescence detection or the maximum spontaneous light force. However, when you are on resonance, there is a divergence which cannot be |
| − | |||
treated by perturbation theory. Nevertheless, there are ways to still | treated by perturbation theory. Nevertheless, there are ways to still | ||
| − | apply diagrams to | + | apply diagrams to derive what happens. We will see that we have to sum up an infinite number of diagrams. Therefore, the problem of resonant scattering is also an excellent non-trivial example to illustrate the diagrammatic approach. At the end of our discussion, we will find the familiar result of the natural linewidth and spontaneous emission, but this time, it is derived from first principles and not in a phenomenological way, as in many textbooks. |
| − | scattering is also an excellent example of | + | |
| − | |||
=== The need for non-perturbative expansion in resonant scattering === | === The need for non-perturbative expansion in resonant scattering === | ||
| − | So far, we have discussed time perturbation theory, and obtained | + | So far, we have discussed time perturbation theory, and obtained the T matrix element <math>T_{fi}</math> |
| − | + | which connects initial and final states. To second order, this result is nothing more than Fermi's golden rule. The result we | |
| − | |||
obtained is | obtained is | ||
:<math>\begin{array}{rcl} | :<math>\begin{array}{rcl} | ||
| Line 24: | Line 21: | ||
</math> | </math> | ||
| − | Resonant scattering | + | Resonant scattering arises when photons are scattered off atoms, and the photon energy is close to the energy difference between ground and excited state of the atom: |
| − | close to the energy difference of | ||
::[[Image:Resonant_scattering-resonant-scattering-fig1.png|thumb|204px|none|]] | ::[[Image:Resonant_scattering-resonant-scattering-fig1.png|thumb|204px|none|]] | ||
| Line 31: | Line 27: | ||
Let <math>\hbar\omega \approx E_b-E_a</math>, and consider a photon of wavevector | Let <math>\hbar\omega \approx E_b-E_a</math>, and consider a photon of wavevector | ||
<math>k</math> and polarization <math>\epsilon</math>. The <math>T</math> matrix for this process is, | <math>k</math> and polarization <math>\epsilon</math>. The <math>T</math> matrix for this process is, | ||
| − | assuming that there is only one intermediate state | + | assuming that there is only one relevant intermediate state, <math>b</math>, |
:<math>\begin{align} | :<math>\begin{align} | ||
T &= \langle a,k',\epsilon'| H_I \frac{1}{E_a + \hbar\omega - H_0} H_I | T &= \langle a,k',\epsilon'| H_I \frac{1}{E_a + \hbar\omega - H_0} H_I | ||
| Line 40: | Line 36: | ||
\,. | \,. | ||
\end{align}</math> | \end{align}</math> | ||
| − | + | What does this expression mean in diagrammatic language? It means that the | |
atom is taken to state <math>b</math>, after absorbing a photon, then after | atom is taken to state <math>b</math>, after absorbing a photon, then after | ||
| − | emitting the photon it goes to state <math>a</math>, the ground state. | + | emitting the photon it goes back to state <math>a</math>, the ground state. |
Physically, since the intermediate state is close to the actual | Physically, since the intermediate state is close to the actual | ||
| − | excited state <math>b</math>, we may | + | excited state <math>b</math>, we may consider replacing <math>H_0</math> with <math>H</math> in the |
| − | above term, | + | above term. Diagrammatically, this means that the atom, after absorbing a photon, is propagating not in the unperturbed state <math>b</math> (eigenstate of <math>H_0</math>), but in a state, which is an eigenstate of <math>H</math>. As we will see later, the main result of this is that the divergence in the denominator is cut off by an additional |
imaginary term, | imaginary term, | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 55: | Line 51: | ||
\,. | \,. | ||
\end{align}</math> | \end{align}</math> | ||
| − | + | ||
| − | + | Many textbooks introduce this result phenomenologically. Let us analyze what is means. For this, we expand the energy | |
| − | denominator | + | denominator into powers of <math>\Gamma</math>, obtaining |
:<math> | :<math> | ||
\frac{1}{\hbar\omega + E_a - E_b + i\hbar (\Gamma/2)} | \frac{1}{\hbar\omega + E_a - E_b + i\hbar (\Gamma/2)} | ||
| Line 64: | Line 60: | ||
Because this is an infinite sum, physically it means that the addition | Because this is an infinite sum, physically it means that the addition | ||
of damping, the <math>\Gamma</math> term, results in an infinite order of | of damping, the <math>\Gamma</math> term, results in an infinite order of | ||
| − | interactions <math>H_I</math> and is thus non-perturbative in nature. | + | interactions <math>H_I</math> and is thus non-perturbative in nature (Note that <math>\Gamma</math>, in lowest order approximation, is quadratic in the interaction operator). |
Let us now do this derivation carefully and rigorously. We follow API | Let us now do this derivation carefully and rigorously. We follow API | ||
| Line 71: | Line 67: | ||
=== Evolution operator and resolvent === | === Evolution operator and resolvent === | ||
| − | We have | + | We have obtained the following exact expression for the time evolution operator from time <math>t'</math> to <math>t</math> is |
:<math>\begin{array}{rcl} | :<math>\begin{array}{rcl} | ||
U(t,t') = U_0(t,t') + \frac{1}{i\hbar} \int_{t'}^{t} dt_1 | U(t,t') = U_0(t,t') + \frac{1}{i\hbar} \int_{t'}^{t} dt_1 | ||
U_0(t,t_1) V U(t_1,t') | U_0(t,t_1) V U(t_1,t') | ||
\end{array}</math> | \end{array}</math> | ||
| − | + | This equation is equivalent to the Schrödinger equation. In perturbation theory, is is solved iteratively. To go beyond perturbative expansions, we need to start from this | |
| − | To go beyond perturbative expansions, we need to start from this | ||
expression and manipulate it. | expression and manipulate it. | ||
| Line 112: | Line 107: | ||
\,, | \,, | ||
\end{align}</math> | \end{align}</math> | ||
| − | where <math>\eta</math> is an | + | where <math>\eta</math> is an infinitesimal number introduced to be able to do a |
contour integration later. This now allows us to turn the integral | contour integration later. This now allows us to turn the integral | ||
equation into an algebraic equation, | equation into an algebraic equation, | ||
| Line 126: | Line 121: | ||
</math> | </math> | ||
where <math>z</math> is a complex number, thus extending <math>G</math> into the complex | where <math>z</math> is a complex number, thus extending <math>G</math> into the complex | ||
| − | plane. This is called a resolvent. | + | plane. This is called a resolvent. Note that the resolvent is directly connected with the time evolution operator through the contour integral |
| − | |||
:<math> | :<math> | ||
U(\tau) = \frac{1}{i2\pi} \oint dz e^{iz\tau/\hbar} G(z) | U(\tau) = \frac{1}{i2\pi} \oint dz e^{iz\tau/\hbar} G(z) | ||
\,. | \,. | ||
</math> | </math> | ||
| − | + | Such integrals are often evaluated using the method of residues. | |
=== Iterative solution === | === Iterative solution === | ||
| Line 152: | Line 146: | ||
</math> | </math> | ||
This is exact, but so general that we must now decide what we'll do | This is exact, but so general that we must now decide what we'll do | ||
| − | with it. | + | with it (or what approximations to apply). |
=== Effect of vacuum interaction on the excited state === | === Effect of vacuum interaction on the excited state === | ||
| Line 159: | Line 153: | ||
<math>E_b</math>. We are interested in the physics of one state of an atom, <math>b</math> | <math>E_b</math>. We are interested in the physics of one state of an atom, <math>b</math> | ||
(the excited state), interacting with the vacuum, and want to obtain a | (the excited state), interacting with the vacuum, and want to obtain a | ||
| − | non-perturbative solution. Thus we seek <math>G_{bb}</math>. The expansion | + | non-perturbative solution. Thus we seek <math>G_{bb}</math> which is related to the time-evolution operator for an atom in state <math>|\phi_b{\rangle}</math>. The expansion |
involved will have energy denominators which diverge when <math>z=E_b</math>. | involved will have energy denominators which diverge when <math>z=E_b</math>. | ||
Recall that <math>z</math> is the complex extension of energy <math>E</math>. So let us | Recall that <math>z</math> is the complex extension of energy <math>E</math>. So let us | ||
take all such terms, which diverge as <math>E</math> approches <math>E_b</math>, and see if | take all such terms, which diverge as <math>E</math> approches <math>E_b</math>, and see if | ||
we can pull out all the divergent terms, leaving the expression for | we can pull out all the divergent terms, leaving the expression for | ||
| − | the resolvent still exact. After all, we know the system has | + | the resolvent still exact. After all, we know the system has a |
resonance, so we seek to pull out the terms describing the resonance, | resonance, so we seek to pull out the terms describing the resonance, | ||
leaving a remainder which describes the effects of the interaction | leaving a remainder which describes the effects of the interaction | ||
| − | with the vacuum. | + | with the vacuum, but does not diverge any more and is therefore tractable. |
==== Approximate solution ==== | ==== Approximate solution ==== | ||
| − | + | We want to use a diagrammatic representation of the divergent | |
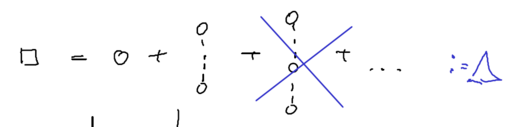
terms. Let us use a symbolic notation for the expansion of the | terms. Let us use a symbolic notation for the expansion of the | ||
resolvent in the energy basis. Let a solid line represent free | resolvent in the energy basis. Let a solid line represent free | ||
| − | propagation in state <math>b</math> (which | + | propagation in state <math>b</math> (which diverges), and a dotted line represent |
propagation in states other than <math>b</math> (which do not diverge). Let a | propagation in states other than <math>b</math> (which do not diverge). Let a | ||
circle represent <math>V</math>. | circle represent <math>V</math>. | ||
| Line 214: | Line 208: | ||
The importance of this result is that: | The importance of this result is that: | ||
<blockquote> | <blockquote> | ||
| − | * The resonant structure of <math>G_{bb}(z)</math> is | + | * The resonant structure of <math>G_{bb}(z)</math> is explicitly accounted for |
* <math>R_b(z)</math> has no divergences near <math>z\approx E_b</math> | * <math>R_b(z)</math> has no divergences near <math>z\approx E_b</math> | ||
* Simple approximations to <math>R_b(z)</math> are possible and correspond to an infinite number of terms in a perturbative expansion. | * Simple approximations to <math>R_b(z)</math> are possible and correspond to an infinite number of terms in a perturbative expansion. | ||
| Line 268: | Line 262: | ||
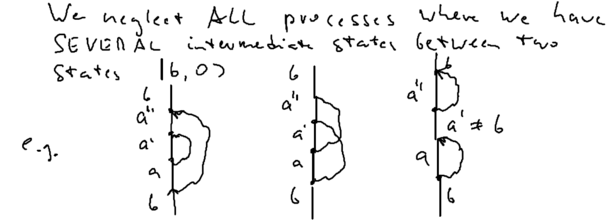
This neglects some higher order interactions; specifically, we neglect | This neglects some higher order interactions; specifically, we neglect | ||
| − | all processes where we have several ( | + | all processes where we have several (i.e. more than one) intermediate |
states, between two states which are both <math>|b,0{\rangle}</math>. For example, we | states, between two states which are both <math>|b,0{\rangle}</math>. For example, we | ||
neglect diagrams such as | neglect diagrams such as | ||
| Line 277: | Line 271: | ||
state with energy <math>E_b</math>. Whenever the atom absorbs the photon and | state with energy <math>E_b</math>. Whenever the atom absorbs the photon and | ||
re-absorbs it, we approximate that it goes back to the state with | re-absorbs it, we approximate that it goes back to the state with | ||
| − | energy <math>E_b</math>. Other processes, we drop because | + | energy <math>E_b</math>. Other processes, we drop because they (intermittently) |
| − | violate energy conservation more than these | + | violate energy conservation more than these leading-order processes. |
Mathematically, this gives us | Mathematically, this gives us | ||
| Line 302: | Line 296: | ||
\,, | \,, | ||
</math> | </math> | ||
| − | where the <math>\Delta_b</math> is now identified as the energy shift | + | where the <math>\Delta_b</math> is now identified as the radiative energy shift (analogous to the Lamb shift), and the imaginary part gives rise to an |
| − | |||
exponential decay at rate <math>\Gamma_b</math>. | exponential decay at rate <math>\Gamma_b</math>. | ||
| Line 315: | Line 308: | ||
is memoryless, to the extent of the approximations used here. | is memoryless, to the extent of the approximations used here. | ||
| − | Note, however, that if we had | + | Note, however, that if we had truncated the infinite perturbation series at some order, we |
would have obtained a polynomial decay, rather than an exponential | would have obtained a polynomial decay, rather than an exponential | ||
| − | decay. Recall that the apparently | + | decay. Recall that the apparently innocous introduction of <math>\Gamma</math> |
| − | into the denominator, as we discussed in our | + | into the denominator, as we discussed in our initial treatment of |
resonant scattering, lead to an infinite order interaction between the | resonant scattering, lead to an infinite order interaction between the | ||
atom and vacuum. | atom and vacuum. | ||
Latest revision as of 23:10, 26 April 2009
There are several important reasons to consider resonant scattering. Resonant scattering is when we have the strongest scattering rate, and as a result, the most sensitive fluorescence detection or the maximum spontaneous light force. However, when you are on resonance, there is a divergence which cannot be treated by perturbation theory. Nevertheless, there are ways to still apply diagrams to derive what happens. We will see that we have to sum up an infinite number of diagrams. Therefore, the problem of resonant scattering is also an excellent non-trivial example to illustrate the diagrammatic approach. At the end of our discussion, we will find the familiar result of the natural linewidth and spontaneous emission, but this time, it is derived from first principles and not in a phenomenological way, as in many textbooks.
Contents
The need for non-perturbative expansion in resonant scattering
So far, we have discussed time perturbation theory, and obtained the T matrix element which connects initial and final states. To second order, this result is nothing more than Fermi's golden rule. The result we obtained is
We can then replace the energy denominator by an expansion
Resonant scattering arises when photons are scattered off atoms, and the photon energy is close to the energy difference between ground and excited state of the atom:
Let , and consider a photon of wavevector and polarization . The matrix for this process is, assuming that there is only one relevant intermediate state, ,
What does this expression mean in diagrammatic language? It means that the atom is taken to state , after absorbing a photon, then after emitting the photon it goes back to state , the ground state. Physically, since the intermediate state is close to the actual excited state , we may consider replacing with in the above term. Diagrammatically, this means that the atom, after absorbing a photon, is propagating not in the unperturbed state (eigenstate of ), but in a state, which is an eigenstate of . As we will see later, the main result of this is that the divergence in the denominator is cut off by an additional imaginary term,
Many textbooks introduce this result phenomenologically. Let us analyze what is means. For this, we expand the energy denominator into powers of , obtaining
Because this is an infinite sum, physically it means that the addition of damping, the term, results in an infinite order of interactions and is thus non-perturbative in nature (Note that , in lowest order approximation, is quadratic in the interaction operator).
Let us now do this derivation carefully and rigorously. We follow API pages 167-174 and 180-189. There are two parts.
Evolution operator and resolvent
We have obtained the following exact expression for the time evolution operator from time to is
This equation is equivalent to the Schrödinger equation. In perturbation theory, is is solved iteratively. To go beyond perturbative expansions, we need to start from this expression and manipulate it.
To cast this expression into a more tractable form we can seek to remove the integrals, by working in the Fourier space. The convolution of two functions, in Fourier space, is the product of the Fourier transforms. This would be useful if the integral were a convolution, but it is not, at least as presented.
A convolution integral must integrate over range , but the above does not have this form. This can be circumventd by not discussing the time evolution operator , but rather, a kind of Green's function,
and similarly for and , where is the Heaviside step function. This allows us to write
Because satisfies a differential equation similar to the Schrödinger equation but with some delta functions in time, is referred to as being the retarded Green's function.
Now take the Fourier transform. Let be the Fourier transform of ,
where is an infinitesimal number introduced to be able to do a contour integration later. This now allows us to turn the integral equation into an algebraic equation,
Define
where is a complex number, thus extending into the complex plane. This is called a resolvent. Note that the resolvent is directly connected with the time evolution operator through the contour integral
Such integrals are often evaluated using the method of residues.
Iterative solution
Let us seek an iterative solution to the algebraic equation we have in hand. This is, for example,
for two iterative steps. This looks and smells like a geometric series, but in order to take advantage of this, we must go from operators to numbers. This can be done by writing the operator equation in terms of eigenfunctions of , with energy and . Now, the matrix element of the resolvent is, in this basis,
This is exact, but so general that we must now decide what we'll do with it (or what approximations to apply).
Effect of vacuum interaction on the excited state
Let us focus on one discrete state, of with energy . We are interested in the physics of one state of an atom, (the excited state), interacting with the vacuum, and want to obtain a non-perturbative solution. Thus we seek which is related to the time-evolution operator for an atom in state . The expansion involved will have energy denominators which diverge when . Recall that is the complex extension of energy . So let us take all such terms, which diverge as approches , and see if we can pull out all the divergent terms, leaving the expression for the resolvent still exact. After all, we know the system has a resonance, so we seek to pull out the terms describing the resonance, leaving a remainder which describes the effects of the interaction with the vacuum, but does not diverge any more and is therefore tractable.
Approximate solution
We want to use a diagrammatic representation of the divergent terms. Let us use a symbolic notation for the expansion of the resolvent in the energy basis. Let a solid line represent free propagation in state (which diverges), and a dotted line represent propagation in states other than (which do not diverge). Let a circle represent .
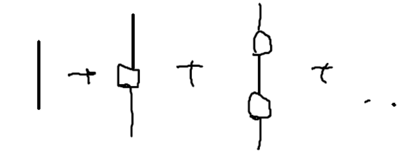
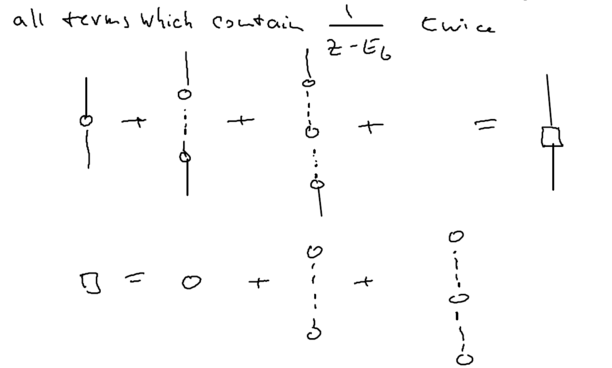
Consider now the diagrams representing all the terms which contain twice:
Let us introduce a square box to represent all such terms, that is, all terms, to infinite order, which do not allow the system to go back to the state . Analytically,
So far, we've isolated all terms with two occurences of the diverging energy denominator. In a similar manner, all terms with occurances can be identified as well. For , for example, a single return to the state is allowed in the intermediate states. Therefore, the contribution of all the terms which have three divergent denominators to is
Generalizing this, we have now found that
because the first equality is a geometric series. This is an exact result. Note that all the complexity now has been moved into the kernel , but this term now has no divergences.
The importance of this result is that:
- The resonant structure of is explicitly accounted for
- has no divergences near
- Simple approximations to are possible and correspond to an infinite number of terms in a perturbative expansion.
The expression for ,
contained the original interaction, the second order expression, and higher order expressions. The exact time propagation was given by:
the free propagator, propagation through once, twice, and so on. is the kernel. Now, we want to make an approximation. We know that is well behaved, so we can cut off the series at the second order. Denote such an approximation by the symbol . The full expression using this still involves an infinite series of diagrams, but we have replaced by :
Application to excited state shift and decay
Let us apply this formulation to an excited atomic state, , which is, more specifically, , the excited atomic state and no photon. With this diagramatic approach, we calculate , the matrix element of with state . Then, through a contour integration, we obtain the time evolution of the state ,
which is the time evolution of the atom in its excited state.
The resolvant is
inserting the second order approximation for , which considers only two atom light interaction vertices:
we obtain the physics due to an atom emitting a photon once and re-absorbing. Thus, we approximate the exact solution for by:
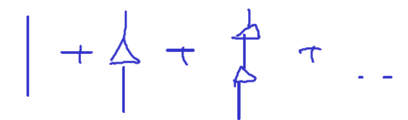
This neglects some higher order interactions; specifically, we neglect all processes where we have several (i.e. more than one) intermediate states, between two states which are both . For example, we neglect diagrams such as
In other words, we have a two-level system, and there is one discrete state with energy . Whenever the atom absorbs the photon and re-absorbs it, we approximate that it goes back to the state with energy . Other processes, we drop because they (intermittently) violate energy conservation more than these leading-order processes.
Mathematically, this gives us
Now we do one more approximation. Recall that we chose this approach because has no pole around . So we can now evaluate this expression at the energy . This gives us an expression for the resolvant,
Doing the backwards Fourier transform (contour integral) to relate this back to the time-evolution operator, we get
where the is now identified as the radiative energy shift (analogous to the Lamb shift), and the imaginary part gives rise to an exponential decay at rate .
Discussion: Relation to the optical Bloch equations
When we neglected the energy dependence of the decay and the radiative shift , this corresponds to assuming a delta function approximation in time. That is the Markov approximation which we have seen previously in the context of the optical Bloch equation. In other words, the vacuum is acting as a reservoir, which is memoryless, to the extent of the approximations used here.
Note, however, that if we had truncated the infinite perturbation series at some order, we would have obtained a polynomial decay, rather than an exponential decay. Recall that the apparently innocous introduction of into the denominator, as we discussed in our initial treatment of resonant scattering, lead to an infinite order interaction between the atom and vacuum.
References
- see API pp. 93-97 and pp. 167-174, 180-189



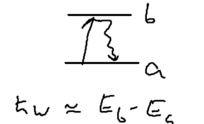
















































![{\displaystyle {\frac {1}{(z-E_{b})^{3}}}\left[{R_{b}(z)}\right]^{2}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ced5cfe97522c1495e90bbf442086b2e3730763f)
![{\displaystyle {\begin{aligned}G_{bb}(z)&={\frac {1}{z-E_{b}}}\sum _{n=0}^{\infty }\left[{\frac {R_{b}(z)}{(z-E_{b})}}\right]^{n}\\&={\frac {1}{z-E_{b}-R_{b}(z)}}\,,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce23c113fcccd59c525342e952d8e7ff63e5eaa7)