imported>Ichuang |
imported>Ichuang |
| Line 1: |
Line 1: |
| − | = Ion traps and quantum information =
| |
| | | | |
| − | Thus far, we have focused our attention on neutral atoms, and their
| |
| − | interactions with the electromagnetic field. Charged atoms are an
| |
| − | important physical system which are also important to study, for a
| |
| − | variety of reasons. They can be confined in with much deeper
| |
| − | potential wells, using electric fields, than is possible with light
| |
| − | forces alone. Ions can also be readily trapped in small numbers,
| |
| − | allowing single atoms or small, discrete numbers of atoms to be
| |
| − | individually manipulated. This capability has made trapped ions an
| |
| − | excellent physical system for creation of exotic quantum states, such
| |
| − | as Schr\"odinger cat superpositions, and highly entangled multi-atom
| |
| − | states. Trapped ions have also proven to be an excellent platform for
| |
| − | implementation of many quantum information protocols, including
| |
| − | teleportation, superdense coding, and quantum error correction; simple
| |
| − | quantum algorithms such as the Deutsch-Jozsa and Grover quantum search
| |
| − | algorithms have also been demonstrated. Efforts are underway in the
| |
| − | community to realize trapped ion systems with not just handfuls, but
| |
| − | rather, hundreds to thousands of individually controlled ion qubits,
| |
| − | in highly integrated trapped ion chips.
| |
| | | | |
| − | This chapter begins with a description of laser cooling in the trapped
| |
| − | ion physical system. We then describe how arbitrary motional states
| |
| − | of ions can be engineered, in the second section. The third section
| |
| − | describes quantum computation with trapped ions, and the fourth
| |
| − | section covers concepts in quantum simulation with ions.
| |
| − |
| |
| − | == Laser cooling of trapped ions ==
| |
| | | | |
| | A simple comparison of potential depths provides useful perspective | | A simple comparison of potential depths provides useful perspective |
A simple comparison of potential depths provides useful perspective
for understanding the experimental convenience of trapped ions versus
neutral atoms. Recall that the depth of a dipole force trap is
 ; for a
; for a  Watt laser at
Watt laser at 
 m focused
to a
m focused
to a 
 m waist used to trap atomic sodium, the trap depth is
m waist used to trap atomic sodium, the trap depth is

 K; this is not much more than the Doppler cooling limit.
A magneto-optical trap is much deeper; for typical laboratory magnetic
field gradients, depths of
K; this is not much more than the Doppler cooling limit.
A magneto-optical trap is much deeper; for typical laboratory magnetic
field gradients, depths of  K can be obtained.
In contrast, a singly charged ion in an electric field of
K can be obtained.
In contrast, a singly charged ion in an electric field of  V/mm, which is easily obtained in the laboratory, the depth of an RF
ion trap can be over
V/mm, which is easily obtained in the laboratory, the depth of an RF
ion trap can be over  K. This allows hot ions to be
readily trapped, and subsequently laser cooled.
K. This allows hot ions to be
readily trapped, and subsequently laser cooled.
A unique aspect of trapped ions, versus neutral atoms, is the
importance of the role of the trapping potential in the laser cooling
process. As the motion of ions is reduced to the characteristic size
of their confining potential, quantum aspects of their motion become
accessible. This allows a form of laser cooling known as {\em
resolved sideband cooling} to be performed, through which ions can be
cooled to their motional ground states.
Physical system
Two kinds of ion traps are widely used. The Penning trap employs
static magnetic and electric fields to confine ions. The Paul trap
employs just oscillating electric fields, and is the configuration we
shall study here.
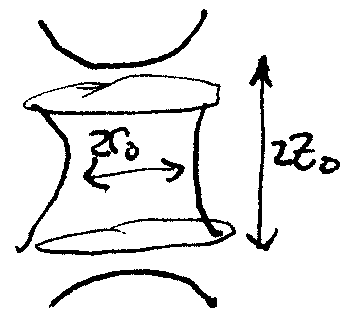
Consider this electrode configuration:
The inner surfaces are hyperboloids, the top and bottom electrodes are
tied together, and the drive voltage oscillates sinusoidally at
frequency  , such that near the center of the electrodes, the
potential is
, such that near the center of the electrodes, the
potential is

For a singly charged ion of mass  located in this trap, the
solutions to the equations of motion balancing the force of the
electric field against ion motion are
located in this trap, the
solutions to the equations of motion balancing the force of the
electric field against ion motion are

This is a Mathieu equation, where

and  is a non-dimensional parameter. When
is a non-dimensional parameter. When  ,
stable solutions exist. These solutions describe a fast oscillation
known as micromotion, superposed on top of a slow harmonic
motion with secular frequency
,
stable solutions exist. These solutions describe a fast oscillation
known as micromotion, superposed on top of a slow harmonic
motion with secular frequency

The amplitude of micromotion, in a well designed experiment, is very
small, and thus can be neglected. The dominant physics of a trapped
ion system are thus described by an atom coupled to a simple harmonic
oscillator.
Typically, RF frequencies are  MHz or higher, and secular
frequencies are
MHz or higher, and secular
frequencies are  MHz. These may be compared with typical
spontaneous emission rates of
MHz. These may be compared with typical
spontaneous emission rates of  MHz, and the recoil
energy from a single photon emission of
MHz, and the recoil
energy from a single photon emission of

where  is the frequency of the laser. The three
systems involved in this scenario are thus the trapped ion, with its
atomic levels, the harmonic oscillator, and incident electromagnetic
radiation on the atom. That is, we have a system of atom + photon +
phonon, where the phonon represents quantized vibrational modes of the
trapped atom.
is the frequency of the laser. The three
systems involved in this scenario are thus the trapped ion, with its
atomic levels, the harmonic oscillator, and incident electromagnetic
radiation on the atom. That is, we have a system of atom + photon +
phonon, where the phonon represents quantized vibrational modes of the
trapped atom.
Hamiltonian: classical field + 2-level atom
Let us model the trapped ion system initially using a classical field,
and neglect spontaneous emission. Let us also approximate the atom to
be a two-level system. The Hamiltonian for such a system has the
interaction
![{\displaystyle {\begin{array}{rcl}H_{I}&=&{\vec {d}}\cdot {\vec {E}}\\&=&\left[{d{\vec {S}}}\right]\cdot \left[{E{\hat {x}}\cos(kz-\omega t)}\right]\,,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88b249de14d5e41f788a686b961f174126a5fb03)
where we use  to denote the spin of the atom, and assume the
electric field is along the
to denote the spin of the atom, and assume the
electric field is along the  direction.
direction.  is the position
of the ion in the field; we quantize this degree of freedom by
representing it as motion in a harmonic oscillator, letting
is the position
of the ion in the field; we quantize this degree of freedom by
representing it as motion in a harmonic oscillator, letting

where  is the characteristic length scale of the harmonic motion.
The interaction Hamiltonian can thus be written as
is the characteristic length scale of the harmonic motion.
The interaction Hamiltonian can thus be written as
![{\displaystyle H_{I}=dES_{x}\cos \left[{kz_{0}(a+a^{\dagger })-\omega t}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e476fd1511b1bd6273cfb45d390b1f2e82fc68a)
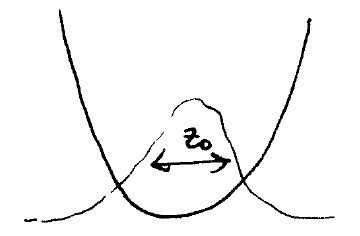
The Lamb-Dicke parameter
When the ions are well-confined, a natural small parameter arises, in
which this interaction can be expanded. This parameter describes the
extent to which the ion is localized in the trap, relative to the
incident light. We define this Lamb-Dicke parameter as

It is the ratio of the size of the ground state wavefunction of the
motion in the harmonic oscillator, to the incident laser wavelength:
\noindent
Note that  can also be understood as being the ratio of the
recoil frequency to the vibrational frequency.
can also be understood as being the ratio of the
recoil frequency to the vibrational frequency.
Expansion in the Lamb-Dicke parameter
Let us now expand  to leading order in
to leading order in  . Recall that
. Recall that  , and let
, and let  be the Rabi
frequency. In terms of these,
be the Rabi
frequency. In terms of these,
![{\displaystyle {\begin{array}{rcl}H_{I}&=&\hbar \Omega \left[{S_{+}+S_{-}}\right]\cos \left[{\eta (a+a^{\dagger })-\omega t}\right]\\&=&{\frac {\hbar \Omega }{2}}\left[{S_{+}+S_{-}}\right]\left[{e^{i\eta (a+a^{\dagger })-\omega t}+e^{-i\eta (a+a^{\dagger })+\omega t}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d938155c229c66f4b2f36beca77b77e8babb3be1)
The exponentials can be expanded to leading order in  , resulting
in terms of the form
, resulting
in terms of the form ![{\displaystyle \left[{1+i\eta (a+a^{\dagger })}\right]e^{-i\omega t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7909df519a9781fb3d0c7d5ce2a3da6a71fb7281) , such
that
, such
that
![{\displaystyle {\begin{array}{rcl}H_{I}&=&{\frac {\hbar \Omega }{2}}\left[{S_{+}e^{-i\omega t}+S_{-}e^{i\omega t}}\right]+{\frac {i\eta \hbar \Omega }{2}}(S_{+}+S_{-})\left[{a+a^{\dagger }}\right]\left({e^{-i\omega t}-e^{i\omega t}}\right)\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76b8afe5bc9450df56aa6ca0332488469e295724)
In the above expansion, it is assumed that the laser's frequency is
close to that of the atomic transition, such that to good
approximation, terms oscillating as  can be dropped (the
rotating wave approximation). The first term in this expression
describes the carrier transition, in which the light changes the
internal atomic state, and the second term describes sideband
transitions, in which the light changes both the internal atomic state
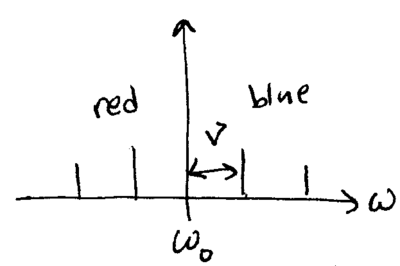
as well as its motional state. These transitions have a frequency
spectrum which looks like:
can be dropped (the
rotating wave approximation). The first term in this expression
describes the carrier transition, in which the light changes the
internal atomic state, and the second term describes sideband
transitions, in which the light changes both the internal atomic state
as well as its motional state. These transitions have a frequency
spectrum which looks like:
Moving into the rotating frame defined by the atom's internal and
motional states simplifies this Hamiltonian, providing a
time-independent form. Let this frame be defined by the system
Hamiltonian

such that in the rotating frame, operators are transformed according
to

The interaction Hamiltonian in this frame is approximated by
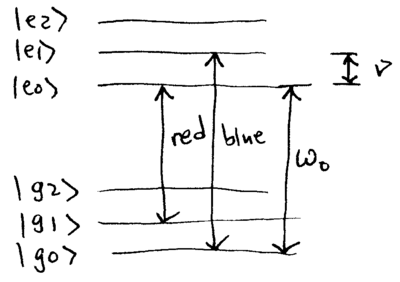
![{\displaystyle {\begin{array}{rcl}H'_{I}&=&e^{iH_{0}t/\hbar }H_{I}e^{-iH_{0}t/\hbar }\\&=&\left\{{\begin{array}{lr}{\frac {\hbar \Omega }{2}}\left[{S_{+}+S_{-}}\right]&{\omega \approx \omega _{0}~~{\rm {carrier}}}\\{\frac {i\eta \hbar \Omega }{2}}(S_{+}a^{\dagger }-S_{-}a)&{\rm {\omega \approx \omega _{0}+\nu ~~{\rm {blue~sideband}}}}\\{\frac {i\eta \hbar \Omega }{2}}(S_{+}a-S_{-}a^{\dagger })&{\rm {\omega \approx \omega _{0}-\nu ~~{\rm {red~sideband}}}}\end{array}}\right.\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1db71d88513f2a7c304214fb5e816603917f6aa)
The first few energy levels are diagrammed here:
Resolved sideband cooling
When the ion is hot, doppler shifts will dominate, and the sidebands
will be unresolvable. However, for many ions, standard doppler
cooling is sufficient to reach the point at which the motional
sidebands become resolvable. In that regime, a different cooling
method can be applied; this method is known as {\em resolved sideband
cooling}.
The basic idea of this method is analogous to optical pumping: the
laser is detuned to cause transitions on the red sideband of the ion,
removing one quantum of motion for each photon absorbed. Just as for
laser cooling of neutral atoms, let us calculate the cooling limit of
such a procedure.
Let  be an eigenstate of the harmonic motion of the ion, with
motional quantum number
be an eigenstate of the harmonic motion of the ion, with
motional quantum number  , and recall that
, and recall that  and
and  . The transition amplitude between
motional states
. The transition amplitude between
motional states  and
and  is given by this matrix element of
the interaction Hamiltonian:
is given by this matrix element of
the interaction Hamiltonian:
![{\displaystyle {\begin{array}{rcl}\langle n\pm 1|H'_{I}|n\rangle \approx \langle n\pm 1|i\eta {\frac {\hbar \Omega }{2}}\left[{{\sqrt {n}}|n-1\rangle \langle n|-{\sqrt {n+1}}|n+1\rangle \langle n|}\right]|n{\rangle }\,,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8ad44051c6b3e2ebf567acd69789c00dcf090b)
in the limit that  is small, and we're interested only in terms
which couple
is small, and we're interested only in terms
which couple  and
and  . Let us define
. Let us define

as the lineshape function; it captures the frequency dependent
response of the atom to a laser detuned by  from the atomic resonance.
from the atomic resonance.
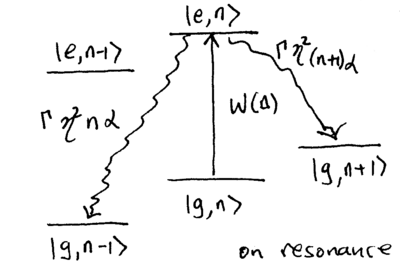
The incident laser light can connect three basic transitions: the
carrier, the blue sideband, and the red sideband. How do those
transitions contribute to changing the motional quantum number  ?
Excitations of the carrier transition couple
?
Excitations of the carrier transition couple  (using
(using  ) to the state
) to the state  , with rate proportional
to
, with rate proportional
to  . The excited state can then decay to
. The excited state can then decay to  or
or
 , changing the motional quantum number; these transitions
occur with rates proportional to
, changing the motional quantum number; these transitions
occur with rates proportional to  and
and  , respectively, where
, respectively, where  is a geometric factor
describing the probability for spontaneous emission to change
is a geometric factor
describing the probability for spontaneous emission to change  .
For dipole emission into free space,
.
For dipole emission into free space,  . These
transitions are diagrammed as follows:
. These
transitions are diagrammed as follows:
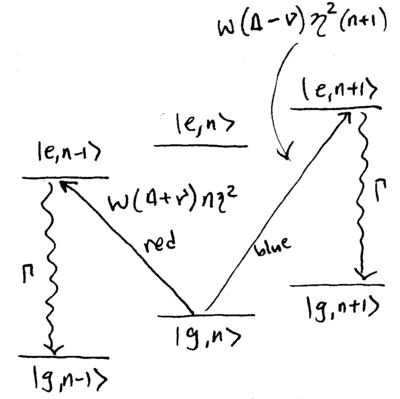
On the blue and red sidebands, absorption happens at a rate
proportional to  and
and  , while spontaneous emission happens at rate
proportional to
, while spontaneous emission happens at rate
proportional to  , all-together connecting
, all-together connecting  with
with
 . These transitions are diagrammed as follows:
. These transitions are diagrammed as follows:
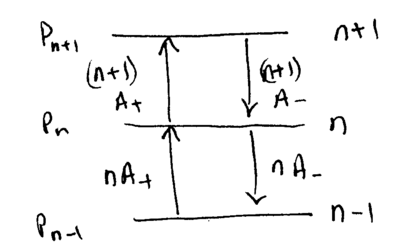
To obtain the cooling limits of resolved sideband cooling, we need to
write down the rate equations for these phonon-number changing carrier
and sideband excitation processes, and solve for the steady state
average phonon number. For the transitions
where  is the probability of being in the
is the probability of being in the  phonon state, the
transition rate coefficients are
phonon state, the
transition rate coefficients are
![{\displaystyle A_{\pm }={\frac {\Omega ^{2}}{\Gamma }}\eta ^{2}\left[{W(\Delta \mp \nu )+\alpha W(\Delta )}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ab62623e908476e76e44ad96cf4d0a6aaa32da1)
The first term in the brackets comes from the sideband excitations,
and the second from the carrier. The rate equations for the
populations are thus
![{\displaystyle {\dot {P}}_{n}=\left[{nP_{n-1}-(n+1)P_{n}}\right]A_{+}+\left[{(n+1)P_{n+1}-nP_{n}}\right]A_{-}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337f828eb099bccb26dc7a4ac03fff0dc9c52600)
The average phonon number  is
is

which evolves as
![{\displaystyle {\begin{array}{rcl}{\frac {d}{dt}}{\bar {n}}&=&A_{-}\left[{\sum _{n}n(n+1)P_{n+1}-n^{2}P_{n}}\right]+A_{+}\left[{\sum _{n}n^{2}P_{n-1}-n(n+1)P_{n}}\right]\\&=&-{\bar {n}}A_{-}+({\bar {n}}+1)A_{+}\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23935219ee9f90f22b0c80793cbd3b95297d4240)
This differential equation has a solution in which  decays
exponentially as
decays
exponentially as  to an equilibrium average phonon
number
to an equilibrium average phonon
number  ,
,

The corresponding equilibrium temperature is given by

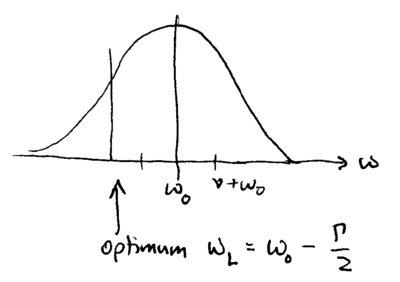
It is insightful to evaluate these expressions in two limits. When
the ion is weakly confined, such that  , then the
sidebands are poorly resolved:
, then the
sidebands are poorly resolved:
The optimum detuning is  , and
cooling corresponds to standard Doppler cooling of free particles,
giving
, and
cooling corresponds to standard Doppler cooling of free particles,
giving

with a final temperature of around

Including geometric factors reduces this slightly, by  .
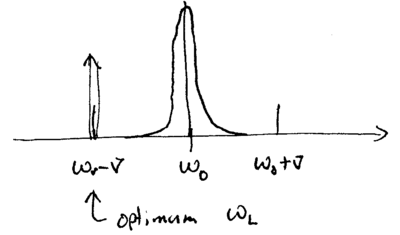
The strong confinement limit is reached when
.
The strong confinement limit is reached when  , so that
individual sidebands are well resolved:
, so that
individual sidebands are well resolved:
This is the case of resolved sideband cooling, as mentioned
above. For this case, the laser is detuned to  , such that
, such that  , and
, and  , such that the equilibrium average phonon number, given by
, such that the equilibrium average phonon number, given by

is approximately  , which is
much less than one. This corresponds to a temperature of
, which is
much less than one. This corresponds to a temperature of

Essentially, the final temperature is set by zero-point motion of the
ion in the harmonic trap.
References






















![{\displaystyle {\begin{array}{rcl}H_{I}&=&{\vec {d}}\cdot {\vec {E}}\\&=&\left[{d{\vec {S}}}\right]\cdot \left[{E{\hat {x}}\cos(kz-\omega t)}\right]\,,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88b249de14d5e41f788a686b961f174126a5fb03)





![{\displaystyle H_{I}=dES_{x}\cos \left[{kz_{0}(a+a^{\dagger })-\omega t}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e476fd1511b1bd6273cfb45d390b1f2e82fc68a)





![{\displaystyle {\begin{array}{rcl}H_{I}&=&\hbar \Omega \left[{S_{+}+S_{-}}\right]\cos \left[{\eta (a+a^{\dagger })-\omega t}\right]\\&=&{\frac {\hbar \Omega }{2}}\left[{S_{+}+S_{-}}\right]\left[{e^{i\eta (a+a^{\dagger })-\omega t}+e^{-i\eta (a+a^{\dagger })+\omega t}}\right]\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d938155c229c66f4b2f36beca77b77e8babb3be1)
![{\displaystyle \left[{1+i\eta (a+a^{\dagger })}\right]e^{-i\omega t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7909df519a9781fb3d0c7d5ce2a3da6a71fb7281)
![{\displaystyle {\begin{array}{rcl}H_{I}&=&{\frac {\hbar \Omega }{2}}\left[{S_{+}e^{-i\omega t}+S_{-}e^{i\omega t}}\right]+{\frac {i\eta \hbar \Omega }{2}}(S_{+}+S_{-})\left[{a+a^{\dagger }}\right]\left({e^{-i\omega t}-e^{i\omega t}}\right)\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76b8afe5bc9450df56aa6ca0332488469e295724)



![{\displaystyle {\begin{array}{rcl}H'_{I}&=&e^{iH_{0}t/\hbar }H_{I}e^{-iH_{0}t/\hbar }\\&=&\left\{{\begin{array}{lr}{\frac {\hbar \Omega }{2}}\left[{S_{+}+S_{-}}\right]&{\omega \approx \omega _{0}~~{\rm {carrier}}}\\{\frac {i\eta \hbar \Omega }{2}}(S_{+}a^{\dagger }-S_{-}a)&{\rm {\omega \approx \omega _{0}+\nu ~~{\rm {blue~sideband}}}}\\{\frac {i\eta \hbar \Omega }{2}}(S_{+}a-S_{-}a^{\dagger })&{\rm {\omega \approx \omega _{0}-\nu ~~{\rm {red~sideband}}}}\end{array}}\right.\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1db71d88513f2a7c304214fb5e816603917f6aa)





![{\displaystyle {\begin{array}{rcl}\langle n\pm 1|H'_{I}|n\rangle \approx \langle n\pm 1|i\eta {\frac {\hbar \Omega }{2}}\left[{{\sqrt {n}}|n-1\rangle \langle n|-{\sqrt {n+1}}|n+1\rangle \langle n|}\right]|n{\rangle }\,,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8ad44051c6b3e2ebf567acd69789c00dcf090b)


















![{\displaystyle A_{\pm }={\frac {\Omega ^{2}}{\Gamma }}\eta ^{2}\left[{W(\Delta \mp \nu )+\alpha W(\Delta )}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ab62623e908476e76e44ad96cf4d0a6aaa32da1)
![{\displaystyle {\dot {P}}_{n}=\left[{nP_{n-1}-(n+1)P_{n}}\right]A_{+}+\left[{(n+1)P_{n+1}-nP_{n}}\right]A_{-}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337f828eb099bccb26dc7a4ac03fff0dc9c52600)


![{\displaystyle {\begin{array}{rcl}{\frac {d}{dt}}{\bar {n}}&=&A_{-}\left[{\sum _{n}n(n+1)P_{n+1}-n^{2}P_{n}}\right]+A_{+}\left[{\sum _{n}n^{2}P_{n-1}-n(n+1)P_{n}}\right]\\&=&-{\bar {n}}A_{-}+({\bar {n}}+1)A_{+}\,.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23935219ee9f90f22b0c80793cbd3b95297d4240)