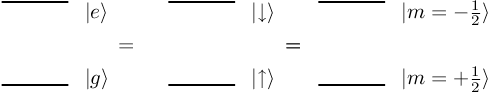imported>Ketterle |
imported>Hmiyake |
| (6 intermediate revisions by 2 users not shown) |
| Line 78: |
Line 78: |
| | <blockquote> | | <blockquote> |
| | ::[[Image:resonances-two-level.png|thumb|500px|none|]] | | ::[[Image:resonances-two-level.png|thumb|500px|none|]] |
| − | Equivalence of two-level system with spin-<math>1/2</math>. Note that for | + | {fig:two_level_spin_half} Equivalence of two-level system with spin-<math>1/2</math>. Note that for |
| | <math>\gamma>0</math> the spin-up state (spin aligned with field) is the ground state. For an electron, with <math>\gamma<0</math>, spin-up is the excited state. Be careful, as both conventions are used in the literature. | | <math>\gamma>0</math> the spin-up state (spin aligned with field) is the ground state. For an electron, with <math>\gamma<0</math>, spin-up is the excited state. Be careful, as both conventions are used in the literature. |
| | </blockquote> | | </blockquote> |
| Line 197: |
Line 197: |
| | where have used the Pauli spin matrices <math>\sigma_x</math>, <math>\sigma_y</math>. The full | | where have used the Pauli spin matrices <math>\sigma_x</math>, <math>\sigma_y</math>. The full |
| | Hamiltonian is thus given by | | Hamiltonian is thus given by |
| | + | |
| | + | :{eq:dressed_atom_hamiltonian} |
| | :<math> | | :<math> |
| | \hat{H}=\frac{\hbar}{2} | | \hat{H}=\frac{\hbar}{2} |
| Line 205: |
Line 207: |
| | </math> | | </math> |
| | This is the famous "dressed atom" Hamiltonian in the so-called "rotating wave | | This is the famous "dressed atom" Hamiltonian in the so-called "rotating wave |
| − | approximation". Its eigenstates and eigenvalues provide a very elegant, very | + | approximation". However, note that in the treatment here there are no approximations; it is exact. Its eigenstates and eigenvalues provide a very elegant, very |
| | intuitive solution to the two-state problem. | | intuitive solution to the two-state problem. |
| | + | |
| | + | === Solution of the Schrodinger Equation for Spin-1/2 in the Rotating Frame === |
| | | | |
| | === Solution of the Schrodinger Equation for Spin-1/2 in the Interaction Representation === | | === Solution of the Schrodinger Equation for Spin-1/2 in the Interaction Representation === |
| Line 254: |
Line 258: |
| | | | |
| | | | |
| − | | + | === "Rapid" Adiabiatic Passage (quantum treatment) === |
| | + | (in the works) |
| | | | |
| | The quantum mechanical treatment yields a probability for non-adiabatic transition (probability for the | | The quantum mechanical treatment yields a probability for non-adiabatic transition (probability for the |
| Line 262: |
Line 267: |
| | </math> | | </math> |
| | in agreement with the qualitative classical criterion derived above. | | in agreement with the qualitative classical criterion derived above. |
| − |
| |
| − | === Atomic Clocks and the Ramsey Method ===
| |
| − | When comparing the Hamiltonian for a spin-<math>1/2</math> in a magnetic field to that of a
| |
| − | two-level system with a coupling between the two levels characterized by the
| |
| − | strength <math>\omega_R</math> and frequency <math>\omega</math>, we see that the energy spacing
| |
| − | between <math> \left|e\right\rangle </math> and <math> \left|g\right\rangle </math> corresponds to the Larmor frequency <math>\omega_0</math>
| |
| − | in the static field. This spacing can provide a frequency or time reference if
| |
| − | perturbations affecting <math>\omega_0</math> are sufficiently well controlled. For
| |
| − | instance, the time unit "second" is defined via the transition frequency
| |
| − | between two hyperfine states in the electronic ground state of the caesium atom,
| |
| − | which is near <math>\unit{9.2}{\giga\hertz}</math> in the microwave domain. The task of an
| |
| − | atomic clock is then to measure this frequency accurately by trying to tune a
| |
| − | frequency source (the frequency <math>\omega</math> of the rotating field <math>B_1</math> in the spin
| |
| − | picture) to the atomic frequency <math>\omega_0</math>. Equivalently, we want to find the
| |
| − | frequency <math>\omega</math> such that the detuning <math>\delta=\omega-\omega_0</math> is equal to
| |
| − | zero.
| |
| − | Starting with an atom in <math> \left|g\right\rangle </math> (spin along <math>+ {\bf{\hat e}} _z</math> for
| |
| − | <math>\gamma>0</math>), we could try to find the resonance frequency by noting that
| |
| − | according to
| |
| − | :<math>
| |
| − | P_e(t)=\frac{\omega_R^2}{\omega_R^2+\delta^2}
| |
| − | sin^2\left(\sqrt{\omega_R^2+\delta^2}\,\frac{t}{2}\right)
| |
| − | </math>
| |
| − | the population of the upper state is maximized for <math>\delta=0</math> (i.e. the
| |
| − | precession of the spin to the <math>- {\bf{\hat e}} _z</math> direction is only complete on
| |
| − | resonance). This is the so-called Rabi method. It suffers from a number of
| |
| − | drawbacks. For one, the signal is only quadratic in the detuning <math>\delta</math>, i.e.
| |
| − | the method is relatively insensitive near <math>\delta=0</math>. Furthermore, the optimum
| |
| − | time <math>t</math> depends on the strength <math>\omega_R</math> of the coupling (i.e. the strength
| |
| − | <math>B_1</math> of the rotating field), so fluctuations in <math>\omega_R</math> can be mistaken for
| |
| − | changes in <math>\delta</math>. Finally the coupling by <math>\omega_R</math> to other levels can
| |
| − | lead to level shifts that are not intrinsic to the atom, but depend on the
| |
| − | applied drive <math>\omega_R</math> (Figure \ref{fig:rabi_third_level}).
| |
| − |
| |
| − | <blockquote>
| |
| − | ::[[Image:resonances-rabi-third-level.png|thumb|400px|none|]]
| |
| − | {fig:rabi_third_level} The drive used for Rabi flopping within the <math>\left|e\right\rangle</math> , <math>\left|g\right\rangle</math> system can also off-resonantly couple one or both levels to other states, perturbing the
| |
| − | transition frequency <math>\omega_0</math>.
| |
| − | </blockquote>
| |
| − |
| |
| − | Norman Ramsey invented an alternative method (the so-called "separated
| |
| − | oscillatory fields method", known for short as the "Ramsey method"
| |
| − | \cite{Ramsey1949,Ramsey1950}, for which he received the Nobel prize), that fixes
| |
| − | all of these problems. It leads to a signal that is linear rather than quadratic
| |
| − | in the detuning <math>\delta</math>, does not require tuning the measurement time to match
| |
| − | the applied field strength <math>\omega_R=\gamma B_1</math>, and, most importantly,
| |
| − | eliminates level shifts due to <math>\omega_R</math> altogether.
| |
| − | The method is as follows. Instead of applying a pulse for a time t that
| |
| − | corresponds to Rabi rotation of the spin by <math>\pi</math> (called a <math>\pi</math> pulse), the
| |
| − | pulse is applied for half that time, corresponding to the Rabi rotation of the
| |
| − | spin by <math>\pi/2</math> into the <math>X-Y</math> plane (<math>\pi/2</math> pulse). Then the applied field
| |
| − | <math>B_1</math> is turned off and the system is left to precess in the static field <math>B_0</math>
| |
| − | (or at its natural frequency <math>\omega_0</math>) for a measurement time <math>T</math>. Finally, a
| |
| − | second <math>\pi/2</math> pulse, identical to the original one, is applied (see Figure
| |
| − | \ref{fig:ramsey_sequence}).
| |
| − |
| |
| − | <blockquote>
| |
| − | ::[[Image:resonances-ramsey-seq.png|thumb|400px|none|]]
| |
| − | {fig:ramsey_sequence} Ramsey sequence
| |
| − | </blockquote>
| |
| − |
| |
| − | The signal is the <math> {\bf{\hat e}} _z</math> component of the spin after the second
| |
| − | interaction. The signal after the second <math>\pi/2</math> pulse is an oscillating signal
| |
| − | in <math>T\delta</math>, depending on how much phase the spin has acquired relative to the
| |
| − | local oscillator (the microwave signal generator at frequency <math>\omega</math>).
| |
| − | Examples of such curves are shown in Figures \ref{fig:ramsey_signal} and
| |
| − | \ref{fig:ramsey_vs_freq}.
| |
| − |
| |
| − | <blockquote>
| |
| − | ::[[Image:resonances-Ramsey.png|thumb|400px|none|]]
| |
| − | {fig:ramsey_signal} Ramsey oscillation signal as a function of time taken in the
| |
| − | Vuleti\'{c} lab in 2007. The drive field was deliberately detuned from
| |
| − | resonance so that the oscillation at the detuning frequency would be visible.
| |
| − | </blockquote>
| |
| − |
| |
| − | <blockquote>
| |
| − | ::[[Image:resonances-Ramsey-vs-freq.png|thumb|400px|none|]]
| |
| − | {fig:ramsey_vs_freq} Experimental data from Ramsey's original paper \cite{Ramsey1950},
| |
| − | showing the signal as a function of frequency. Note the narrow oscillation,
| |
| − | whose width is set by the measurement time <math>T</math>, superimposed on the much broader
| |
| − | background set up by the inhomogeneously broadened <math>\pi/2</math> pulses.
| |
| − | </blockquote>
| |
| − |
| |
| − | At the zero crossings we have maximum sensitivity of the signal with respect to
| |
| − | frequency changes. Note that the signal as a function of <math>T</math> looks similar to
| |
| − | Rabi flopping. However, there the zero crossing measure the Rabi frequency, not
| |
| − | <math>\delta=\omega-\omega_0</math>.
| |
Equation of Motion for the Expectation Value
For the system we have been considering, the Hamiltonian is

Recalling the Heisenberg equation of motion for any operator
 is
is
![{\displaystyle {\frac {d}{dt}}{\hat {O}}={\frac {i}{\hbar }}\left[{\hat {H}},{\hat {O}}\right]+{\frac {\partial {\hat {O}}}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae5069cad777556e25ef2674f2ed7f1fbdc641a0)
where the last term refers to operators with an explicit time dependence, we
have in this instance
![{\displaystyle {\frac {d}{dt}}{\hat {\mu }}_{k}=\gamma {\frac {d}{dt}}{\hat {L}}_{k}={\frac {i\gamma }{\hbar }}\left[{\hat {H}},{\hat {L}}_{k}\right]=-{\frac {i\gamma ^{2}}{\hbar }}B_{0}\left[{\hat {L}}_{z},{\hat {L}}_{k}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31c5220d2321caf92920986550a99c6ba69fb523)
Using ![{\displaystyle \left[{\hat {L}}_{k},{\hat {L}}_{l}\right]=i\hbar \epsilon _{klm}{\hat {L}}_{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b0dce00bc29fe901e80ab62151d3d46ed0adb58) with the
Levi-Civita symbol
with the
Levi-Civita symbol  , we have
, we have

or in short

These are just like the classical equations of motion
\ref{eq:classical_precession_in_static_field}, but here they describe the
precession of the operator for the magnetic moment  or for the
angular momentum
or for the
angular momentum  about the magnetic field at the (Larmor)
angular frequency
about the magnetic field at the (Larmor)
angular frequency  .
.
Note that:
- Just as in the classical model, these operator equations are exact; we have not neglected any higher order terms.
- Since the equations of motion hold for the operator, they must hold for the expectation value

- We have not made use of any special relations for a spin-
 system, but just the general commutation relation for angular momentum. Therefore the result, precession about the magnetic field at the Larmor frequency, remains true for any value of angular momentum
system, but just the general commutation relation for angular momentum. Therefore the result, precession about the magnetic field at the Larmor frequency, remains true for any value of angular momentum  .
.
- A spin-
 system has two energy levels, and the two-level problem with coupling between two levels can be mapped onto the problem for a spin in a magnetic field, for which we have developed a good classical intuition.
system has two energy levels, and the two-level problem with coupling between two levels can be mapped onto the problem for a spin in a magnetic field, for which we have developed a good classical intuition.
- If coupling between two or more angular momenta or spins within an atom results in an angular momentum
 , the time evolution of this angular momentum in an external field is governed by the same physics as for the two-level system. This is true as long as the applied magnetic field is not large enough to break the coupling between the angular momenta; a situation known as the Zeeman regime. Note that if the coupled angular momenta have different gyromagnetic ratios, the gyromagnetic ratio for the composite angular momentum is different from those of the constituents.
, the time evolution of this angular momentum in an external field is governed by the same physics as for the two-level system. This is true as long as the applied magnetic field is not large enough to break the coupling between the angular momenta; a situation known as the Zeeman regime. Note that if the coupled angular momenta have different gyromagnetic ratios, the gyromagnetic ratio for the composite angular momentum is different from those of the constituents.
- For large magnetic field the interaction of the individual constituents with the magnetic field dominates, and they precess separately about the magnetic field. This is the Paschen-Back regime.
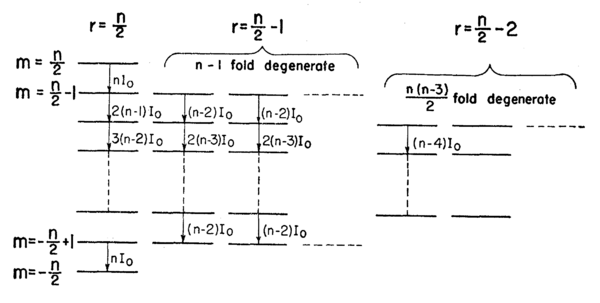
- An even more interesting composite angular momentum arises when
 two-level atoms are coupled symmetrically to an external field. In this case we have an effective angular momentum
two-level atoms are coupled symmetrically to an external field. In this case we have an effective angular momentum  for the symmetric coupling:
for the symmetric coupling:
Level structure diagram for  two-level atoms in a basis of symmetric states \cite{Dicke1954}. The leftmost column corresponds to an effective spin-
two-level atoms in a basis of symmetric states \cite{Dicke1954}. The leftmost column corresponds to an effective spin- object. Other columns correspond to manifolds of symmetric states of the
object. Other columns correspond to manifolds of symmetric states of the  atoms with lower total effective angular momentum.
atoms with lower total effective angular momentum.
- Again the equation of motion for the composite angular momentum
 is a precession. This is the problem considered in Dicke's famous paper \cite{Dicke1954}, in which he shows that this collective precession can give rise to massively enhanced couplings to external fields ("superradiance") due to constructive interference between the individual atoms.
is a precession. This is the problem considered in Dicke's famous paper \cite{Dicke1954}, in which he shows that this collective precession can give rise to massively enhanced couplings to external fields ("superradiance") due to constructive interference between the individual atoms.
The Two-Level System: Spin-1/2
Let us now specialize to the two-level system and calculate the time evolution
of the occupation probabilities for the two levels.
{fig:two_level_spin_half} Equivalence of two-level system with spin- . Note that for
. Note that for
 the spin-up state (spin aligned with field) is the ground state. For an electron, with
the spin-up state (spin aligned with field) is the ground state. For an electron, with  , spin-up is the excited state. Be careful, as both conventions are used in the literature.
, spin-up is the excited state. Be careful, as both conventions are used in the literature.
We have that

where in the last equation we have used the fact that  . The signs
are chosen for a spin with
. The signs
are chosen for a spin with  , such as a proton (Figure
\ref{fig:two_level_spin_half}). For an electron, or any other spin with
, such as a proton (Figure
\ref{fig:two_level_spin_half}). For an electron, or any other spin with
 , the analysis would be the same but for the opposite sign of
, the analysis would be the same but for the opposite sign of  and the corresponding exchange of
and the corresponding exchange of  and
and  . If the system is
initially in the ground state,
. If the system is
initially in the ground state,  (or the spin along
(or the spin along
 ,
,  ), the expectation value obeys the classical
equation of motion \ref{eq:classical_rabi_flopping}:
), the expectation value obeys the classical
equation of motion \ref{eq:classical_rabi_flopping}:
- {eqn:rabi_transition_probability}

Equation \ref{eqn:rabi_transition_probability} is the probability to find system
in the excited state at time  if it was in ground state at time
if it was in ground state at time  .
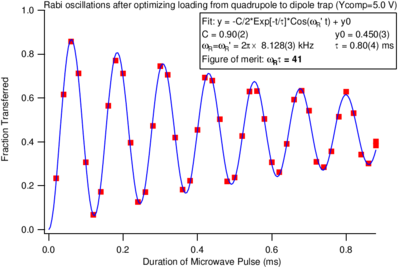
Figure \ref{fig:rabi_signal} shows a real-world example of such an oscillation.
.
Figure \ref{fig:rabi_signal} shows a real-world example of such an oscillation.
{fig:rabi_signal} Rabi oscillation signal taken in the Vuleti\'{c} lab shortly after this
topic was covered in lecture in 2008. The amplitude of the oscillations decays
with time due to spatial variations in the strength of the drive field (and
hence of the Rabi frequency), so that the different atoms drift out of phase
with each other.
Matrix form of Hamiltonian
With the matrix representation

we can write the Hamiltonian  associated with the static
field
associated with the static
field  as
as

where  is the Larmor frequency, and
is the Larmor frequency, and

is a Pauli spin matrix. The eigenstates are  ,
,  with
eigenenergies
with
eigenenergies  . A spin initially
along
. A spin initially
along  , corresponding to
, corresponding to

evolves in time as

which describes a precession with angluar frequency  .
The field
.
The field  , rotating at
, rotating at  in the
in the  plane corresponds to
plane corresponds to

where have used the Pauli spin matrices  ,
,  . The full
Hamiltonian is thus given by
. The full
Hamiltonian is thus given by
- {eq:dressed_atom_hamiltonian}

This is the famous "dressed atom" Hamiltonian in the so-called "rotating wave
approximation". However, note that in the treatment here there are no approximations; it is exact. Its eigenstates and eigenvalues provide a very elegant, very
intuitive solution to the two-state problem.
Solution of the Schrodinger Equation for Spin-1/2 in the Rotating Frame
Solution of the Schrodinger Equation for Spin-1/2 in the Interaction Representation
The interaction representation consists of expanding the state  in terms of the eigenstates
in terms of the eigenstates  ,
,  of the Hamiltonian
of the Hamiltonian  ,
including their known time dependence
,
including their known time dependence  due to
due to  .
That means we write here
.
That means we write here

Substituting this into the Schrodinger equation

then results in the equations of motion for the coefficients

Where we have used the matrix form of the Hamiltonian,
\ref{eq:dressed_atom_hamiltonian}. Introducing the detuning
 , we have
, we have

The explicit time dependence can be eliminated by the sustitution

As you will show (or have shown) in the problem set, this leads to solutions for
 given by
given by

with two constants that are determined by the initial conditions.
For  we find
we find

as already derived from the fact that the expectation value for
the magnetic moment obeys the classical equation.
"Rapid" Adiabiatic Passage (quantum treatment)
(in the works)
The quantum mechanical treatment yields a probability for non-adiabatic transition (probability for the
magnetic moment not following the magnetic field) given by

in agreement with the qualitative classical criterion derived above.


![{\displaystyle {\frac {d}{dt}}{\hat {O}}={\frac {i}{\hbar }}\left[{\hat {H}},{\hat {O}}\right]+{\frac {\partial {\hat {O}}}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae5069cad777556e25ef2674f2ed7f1fbdc641a0)
![{\displaystyle {\frac {d}{dt}}{\hat {\mu }}_{k}=\gamma {\frac {d}{dt}}{\hat {L}}_{k}={\frac {i\gamma }{\hbar }}\left[{\hat {H}},{\hat {L}}_{k}\right]=-{\frac {i\gamma ^{2}}{\hbar }}B_{0}\left[{\hat {L}}_{z},{\hat {L}}_{k}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31c5220d2321caf92920986550a99c6ba69fb523)
![{\displaystyle \left[{\hat {L}}_{k},{\hat {L}}_{l}\right]=i\hbar \epsilon _{klm}{\hat {L}}_{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b0dce00bc29fe901e80ab62151d3d46ed0adb58)