Solutions of the optical Bloch equations

Steady-state solutions

The optical Bloch equations provide a time-dependent quantum description of a spontaneously emitting atom driven by a classical electromagnetic field. Considerable insight into the physical processes involved can be gained by studying these equations in the transient excitation limit, as well as the steady-state limit, as we see in this section. We begin by considering the coherent part of the evolution, then extend this to re-visit the Bloch sphere picture of the optical Bloch equations, which provides useful visualizations of transient responses and steady state solutions.

▼ Category:8.422

► Category:Quantum Light

► Category:Optical Bloch Equations

► Category:Bose-Einstein condensates

► Category:Ion traps and quantum information

► Category:Light forces

► Category:Photon-atom interactions

  Introduction to Atomic Physics

  Quantum light: states and dynamics

  Optical Bloch equations

  Photon-atom interactions

  Frontiers in Atomic Physics

  Ion traps and quantum information

  Quantum gases

Eigenstates of the Jaynes-Cummings Hamiltonian

The optical Bloch equations are

${\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho -2\sigma _{-}\rho \sigma _{+}+\rho \sigma _{+}\sigma _{-}}\right]\,,$

where the Hamiltonian is

$H={\frac {\hbar \omega _{0}}{2}}(|e\rangle \langle e|-|g\rangle \langle g|)+{\frac {\hbar \Omega }{2}}(|g\rangle \langle e|+|e\rangle \langle g|)\,.$

Useful limits to this equation of motion can be obtained, for example, by solving for $\rho$ in the steady state, when ${\dot {\rho }}=0$. Both the Hamiltonian part of this equation, and the damping part, are important to consider, and we begin here by reviewing the coherent evolution under $H$. $H$ arises from the Jaynes-Cummings interaction we have previously considered in the context of cavity QED, describing a single two-level atom interacting with a single mode of the electromagnetic field:

$H_{JC}={\frac {\hbar \omega _{0}}{2}}\left[{|e\rangle \langle e|-|g\rangle \langle g|}\right]+\hbar \omega a^{\dagger }a+{\frac {\hbar \Omega }{2}}\left[{|g\rangle \langle e|+|e\rangle \langle g|}\right]\left[{a+a^{\dagger }}\right]\,.$

The last term in this expression is $H_{I}$, the dipole interaction between atom and field. By defining $\sigma _{+}=|e\rangle \langle g|$ and $\sigma _{-}=|g\rangle \langle e|$, we may write this interaction as

$H_{I}={\frac {\hbar \Omega }{2}}\left[{\sigma _{+}+\sigma _{-}}\right]\left[{a+a^{\dagger }}\right]\,.$

In the frame of reference of the atom and field, recall that

${\begin{array}{rcl}\sigma _{+}a^{\dagger }&\rightarrow &e^{i(\omega +\omega _{0})t}\sigma _{+}a^{\dagger }\\\sigma _{-}a&\rightarrow &e^{-i(\omega +\omega _{0})t}\sigma _{-}a\\\sigma _{+}a&\rightarrow &e^{i(\omega _{0}-\omega )t}\sigma _{+}a\\\sigma _{-}a^{\dagger }&\rightarrow &e^{-i(\omega _{0}-\omega _{0})t}\sigma _{-}a^{\dagger }\,.\end{array}}$

When near resonance, $\omega \approx \omega _{0}$, and because the $\sigma _{+}a^{\dagger }$ and $\sigma _{-}a$ terms oscillate at nearly twice the frequency of $\omega$, those terms can be dropped. Doing so is known as the rotating wave approximation, and it gives us a simplified interaaction Hamiltonian

$H_{I}={\frac {\hbar \Omega }{2}}\left[{a^{\dagger }\sigma _{+}+a\sigma _{-}}\right]\,.$

Under this approximation, it is useful to note that this interaction merely exchanges one quantum of excitation from atom to field, and back, so that the total number of excitations $N=a^{\dagger }a+|e\rangle \langle e|$ is a constant of the motion. We may thus write the total Hamiltonian, in the rotating wave approximation, as

$H=\hbar \omega N+\delta \sigma _{z}+{\frac {\hbar \Omega }{2}}(a^{\dagger }\sigma _{-}+a\sigma _{+})\,,$

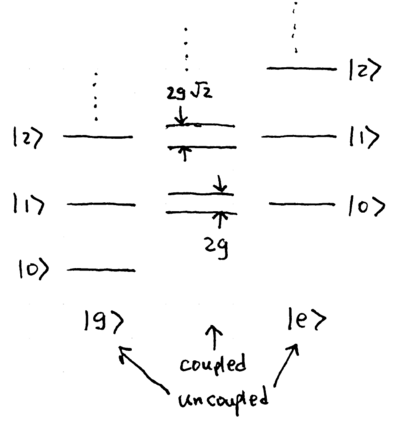
where we have defined $\sigma _{z}=|e\rangle \langle e|-|g\rangle \langle g|$, and $\delta =\omega _{0}-\omega$. Below, we may use $g=\hbar \Omega /2$ to simplify writing. What are the eigenstates of this Hamiltonian? It describes a two-level system coupled to a simple harmonic oscillator; when uncoupled, if $\delta =0$, then the eigenstates are simply those of $|e{\rangle }$, $|g{\rangle }$ and $|n{\rangle }$, as shown here:

\noindent When coupled, degenerate energy levels split, with harmonic oscillator levels $|n{\rangle }$ and $|n+1{\rangle }$ splitting into two energy levels separated by $2g{\sqrt {n+1}}$. Since the coupling only pairs levels separated by one quantum of excitation, it is straightforward to show that the eigenstates of the Jaynes-Cummings Hamiltonian fall into well defined pairs of states, which we may label as $|\pm ,n{\rangle }$; these are

$|\pm ,n\rangle ={\frac {1}{\sqrt {2}}}\left[{|e,n\rangle \pm |g,n+1\rangle }\right]\,,$

and they have energies

$E_{\pm ,n}=\hbar \omega (n+1)\pm g{\sqrt {n+1}}\,.$

When $\delta \neq 0$, similar physics result, but with slightly more complicated expressions describing the eigenstates, as we shall see when we later return to the "dressed states" picture.

Strongly driven atom: Mollow triplet

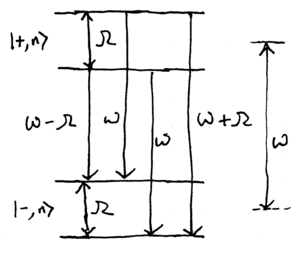
An atom strongly coupled to a single mode electromagnetic field, or an atom driven strongly by a single mode field, will thus have an emission spectrum described by the coupled energy level diagram:

\noindent where, to good approximation, the energy level differences are $\omega$ and $\omega \pm \Omega$. These three lines which appear in the spectrum are known as the Mollow triplet:

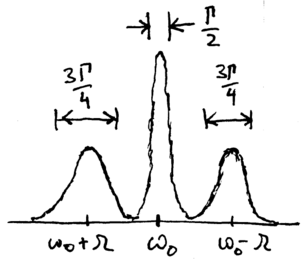
The Mollow triplet is experimentally observed in a wide variety of systems. However, while our energy eigenstate analysis has predicted the number and frequencies of the emission lines, it fails to explain a key characteristic: the widths are not the same. If the central peak at $\omega _{0}$ has width $\Gamma /2$, the two sidebands each have a width of $3\Gamma /4$. To explain this, we need the optical Bloch equations.

Rotating frame of reference for atom + field

A simplification worth using in the study of the optical Bloch equations is a transformation into the rotating frame of the light field. The Hamiltonian for the atom + classical field may be written in general as

$H={\frac {\omega _{0}}{2}}Z+g(X\cos \omega t+Y\sin \omega t)\,,$

where $g$ parameterizes the strength field, $\omega _{0}$ is the atomic transition frequency, and $X,Y,Z$ are the Pauli matrices as usual. Define $|\phi (t)\rangle =e^{i\omega tZ/2}|\chi (t){\rangle }$, such that the Schr\"odinger equation

$i\partial _{t}|\chi (t)\rangle =H|\chi (t){\rangle }$

can be re-expressed as

$i\partial _{t}|\phi (t){\rangle }=\left[{e^{i\omega Zt/2}He^{-i\omega Zt/2}-{\frac {\omega }{2}}Z}\right]|\phi (t){\rangle }\,.$

Since

$e^{i\omega Zt/2}Xe^{-i\omega Zt/2}=(X\cos \omega t-Y\sin \omega t)\,,$

Eq.(\ref{eq:nmr:schrB}) simplifies to become

$i\partial _{t}|\phi (t){\rangle }=\left[{{\frac {\omega _{0}-\omega }{2}}Z+gX}\right]|\phi (t){\rangle }\,,$

where the terms on the right multiplying the state can be identified as the effective `rotating frame' Hamiltonian. The solution to this equation is

$|\phi (t)\rangle =e^{i\left[{{\frac {\omega _{0}-\omega }{2}}Z+gX}\right]t}|\phi (0){\rangle }\,.$

The concept of resonance arises from the behavior of this time evolution, which can be understood as being a single qubit rotation about the axis

${\hat {n}}={\frac {{\hat {z}}+{\frac {2g}{\omega _{0}-\omega }}\,{\hat {x}}}{\sqrt {1+\left({\frac {2g}{\omega _{0}-\omega }}\right)^{2}}}}$

by an angle

$|{\vec {n}}|=t{\sqrt {\left({\frac {\omega _{0}-\omega }{2}}\right)^{2}+g^{2}}}\,.$

When $\omega$ is far from $\omega _{0}$, the qubit is negligibly affected by the laser field; the axis of its rotation is nearly parallel with ${\hat {z}}$, and its time evolution is nearly exactly that of the free atom Hamiltonian. On the other hand, when $\omega _{0}\approx \omega$, the free atom contribution becomes negligible, and a small laser field can cause large changes in the state, corresponding to rotations about the ${\hat {x}}$ axis. The enormous effect a small field can have on the atom, when tuned to the appropriate frequency, is responsible for the concept of atomic `resonance,' as well as nuclear magnetic resonance.

Bloch vector evolution

We have previously seen that an arbitrary qubit state $|\psi \rangle =\cos \theta |0\rangle +e^{i\phi }\sin \phi |1{\rangle }$ can be represented as being a point on a unit sphere, located at $(\theta ,\phi )$ in polar coordinates. Similarly, a density matrix $\rho$ may be depicted as being a point inside or on the unit sphere, using

$\rho ={\frac {I+{\vec {r}}\cdot {\sigma }}{2}}\,,$

where ${\vec {r}}$ is the Bloch vector representation of $\rho$. Explicitly, if we let

$\rho =\left[{\begin{array}{cc}{\rho _{ee}}&{\rho _{eg}}\\{\rho _{ge}}&{\rho _{gg}}\end{array}}\right]\,,$

then

${\begin{array}{rcl}r_{x}&=&\rho _{ge}+\rho _{eg}\\r_{y}&=&(\rho _{ge}-\rho _{eg})/i\\r_{z}&=&\rho _{gg}-\rho _{ee}\,.\end{array}}$

Visulization of the evolution of a density matrix under the optical Bloch equations is thus helped by rewriting them in terms of a differential equation for ${\vec {r}}$. A convenient starting point for this is the optical Bloch equation

${\dot {\rho }}=-{\frac {i}{\hbar }}[H,\rho ]-{\frac {\Gamma }{2}}\left[{\sigma _{+}\sigma _{-}\rho -2\sigma _{-}\rho \sigma _{+}+\rho \sigma _{+}\sigma _{-}}\right]\,,$

using the rotating frame Hamiltonian (suppressing $\hbar$)

$H={\frac {\delta }{2}}Z+gX\,.$

This gives us the equations of motion

${\begin{array}{rcl}{\dot {r}}_{x}&=&\delta \,r_{y}-{\frac {\Gamma }{2}}r_{x}\\{\dot {r}}_{y}&=&-\delta \,r_{x}-g\,r_{z}-{\frac {\Gamma }{2}}r_{y}\\{\dot {r}}_{z}&=&g\,r_{y}-\Gamma (r_{z}-1)\,.\end{array}}$

Note how these equations of motion provide a simple set of flows on the Bloch sphere: the $\delta$ terms correspond to a rotation in the ${\hat {x}}-{\hat {y}}$ plane, $g$ corresponds to a rotation in the ${\hat {y}}-{\hat {z}}$ plane, and $\Gamma$ drives a relaxation process which shrinks ${\hat {x}}$ and ${\hat {y}}$ components of the Bloch vector, while moving the ${\hat {z}}$ component toward $r_{z}=1$. Physically, what is the meaning of $r_{x}$, $r_{y}$, and $r_{z}$? $r_{z}$ is manifestly the population difference between the excited and ground states. The other two components may be interpreted by recognizing that the average dipole moment of the atom is

${\begin{array}{rcl}\langle d\rangle &=&d_{ge}{\rm {Tr}}(\rho (|e\rangle \langle g|+|g\rangle \langle e|))\\&=&d_{ge}(\rho _{ge}e^{i\omega t}+\rho _{eg}e^{-i\omega t})\\&=&d_{ge}(r_{x}\cos \omega t+r_{y}\sin \omega t)\,.\end{array}}$

Thus, $r_{x}$ and $r_{y}$ correspond to the phase components of the atomic dipole moment which are in-phase and in quadrature with the incident electromagnetic field.

Transient repsonse of the optical Bloch equations

The optical Bloch equations allow us to study the internal state of the atom as it changes due to the external driving field, and due to spontaneous emission. Starting from the time-independent form of the equations,

${\begin{array}{rcl}{\dot {r}}_{x}&=&\delta \,r_{y}-{\frac {\Gamma }{2}}r_{x}\\{\dot {r}}_{y}&=&-\delta \,r_{x}-g\,r_{z}-{\frac {\Gamma }{2}}r_{y}\\{\dot {r}}_{z}&=&g\,r_{y}-\Gamma (r_{z}-1)\,,\end{array}}$

we may note that when $g\rightarrow 0$ and at resonance, $\delta =0$, the Bloch vector exhibits pure damping behavior, towards $r_{z}=1$, and $r_{x}=r_{y}=0$. When $g\gg \Gamma$, Rabi oscillations occur, represnted by rapid rotations of the Bloch vector about ${\hat {x}}$. Since the relaxation along ${\hat {y}}$ occurs at rate $\Gamma /2$, and the relaxation about ${\hat {z}}$ occurs at rate $\Gamma$, we might expect that the average relaxation rate of the rotating components under such a strong driving field would be $(\Gamma +\Gamma /2)/2=3\Gamma /4$. The remaining component $r_{x}$ does not rotate, because it sits along ${\hat {x}}$, the axis of rotation. Thus, it relaxes with rate $\Gamma /2$. Computation of the eigenvalues of the equations of motion verify this qualitative picture, and show that for $g\gg \Gamma$, and $\delta =0$, the eigenvalues of motion are $\pm ig+3\Gamma /4$ and $\Gamma /2$. These correspond to a main peak at $\omega _{0}$ with width $\Gamma /2$, and two sidebands at $\omega _{0}\pm \Omega$, with widths $3\Gamma /4$, thus explaining the widths of the observed Mollow triplet lines.

Steady-state solution of the optical Bloch equations

The steady state solution of the optical Bloch equations are found by setting all the time derivatives to zero, giving a set of three simultaneous equations,

${\begin{array}{rcl}0&=&\delta \,r_{y}-{\frac {\Gamma }{2}}r_{x}\\0&=&-\delta \,r_{x}-g\,r_{z}-{\frac {\Gamma }{2}}r_{y}\\0&=&g\,r_{y}-\Gamma (r_{z}-1)\,.\end{array}}$

The solutions are (up to overall minus signs which can be absorbed into definitions):

${\begin{array}{rcl}r_{x}&=&(g\delta ){\frac {1}{\delta ^{2}+g^{2}/2+(\Gamma /2)^{2}}}\\r_{y}&=&\left({\frac {g\Gamma }{2}}\right){\frac {1}{\delta ^{2}+g^{2}/2+(\Gamma /2)^{2}}}\\r_{z}&=&\left(\delta ^{2}+{\frac {\Gamma ^{2}}{4}}\right){\frac {1}{\delta ^{2}+g^{2}/2+(\Gamma /2)^{2}}}\end{array}}$

Physically, these are Lorentzians; the $r_{y}$ solution (the component in quadrature with the dipole) corresponds to an absorption curve with half-width

${\sqrt {{\frac {\Gamma ^{2}}{4}}+{\frac {g^{2}}{2}}}}\,,$

and the $r_{x}$ solution (the component in-phase with the dipole) corresponds to a dispersion curve. And under a strong driving field, as $g\rightarrow \infty$, $r_{z}\rightarrow 0$, indicating that the populations in the excited and ground states are equalizing. The steady-state population in the excited state is

$\rho _{ee}={\frac {1-r_{z}}{2}}={\frac {g^{2}/4}{\delta ^{2}+g^{2}/2+\Gamma ^{2}/4}}\,,$

an important result that will later be used in studying light forces. These solutions can be re-expressed in a simplified manner by defining the saturation parameter

$s={\frac {g^{2}/2}{\delta ^{2}+\Gamma ^{2}/4}}\,,$

in terms of which we find

${\begin{array}{rcl}r_{x}&=&{\frac {2\delta }{g}}{\frac {s}{1+s}}\\r_{y}&=&{\frac {\Gamma }{g}}{\frac {s}{1+s}}\\r_{z}&=&{\frac {1}{1+s}}\,.\end{array}}$

As $s\rightarrow \infty$, the atomic transitions become {\em saturated}, and the linewidth of the transition broadens from its natural value $\Gamma$, becoming $\Gamma '=\Gamma {\sqrt {1+s}}$ on resonance, at $\delta =0$.