Difference between revisions of "Method of Separated Oscillatory Fields"
imported>Ichuang (New page: The separated oscillatory field (SOF) technique is one of the most powerful methods of precision spectroscopy. As the name suggests, it involves two sequential applications of the transit...) |
imported>Ichuang |
||
| Line 34: | Line 34: | ||
single Rabi coil of the same length would produce approximately the same | single Rabi coil of the same length would produce approximately the same | ||
resonance width. | resonance width. | ||
| + | |||
The transition probability for the Ramsey method can be calculated by | The transition probability for the Ramsey method can be calculated by | ||
straightforward application of the formalism presented earlier. Details are | straightforward application of the formalism presented earlier. Details are | ||
| Line 82: | Line 83: | ||
the system is at resonance, in which case the spin's orientation | the system is at resonance, in which case the spin's orientation | ||
is now along <math>\hat{y}</math> in the rotating coordinate system). | is now along <math>\hat{y}</math> in the rotating coordinate system). | ||
| + | |||
During the field-free time <math>T</math>, the spin precesses merrily about | During the field-free time <math>T</math>, the spin precesses merrily about | ||
the constant field <math>B_0</math> between the two oscillating-field | the constant field <math>B_0</math> between the two oscillating-field | ||
| Line 91: | Line 93: | ||
<math>\delta\omega\tau \ll 1</math>) then the spin will have precessed about | <math>\delta\omega\tau \ll 1</math>) then the spin will have precessed about | ||
<math>\hat{z}_0</math> an angle <math>\pi</math> less far than the oscillating field. | <math>\hat{z}_0</math> an angle <math>\pi</math> less far than the oscillating field. | ||
| + | |||
It will consequently lie in the -<math>\hat{y}^\prime</math> direction rather | It will consequently lie in the -<math>\hat{y}^\prime</math> direction rather | ||
than in the <math>\hat{y}^\prime</math> direction in the coordinate system | than in the <math>\hat{y}^\prime</math> direction in the coordinate system | ||
| Line 100: | Line 103: | ||
with period <math>\Delta \omega = 2\pi /T</math>. The central maximum of | with period <math>\Delta \omega = 2\pi /T</math>. The central maximum of | ||
this interference pattern is centered at <math>\omega_0</math> and its full | this interference pattern is centered at <math>\omega_0</math> and its full | ||
| − | width at half maximum (in <math>\omega</math>-space) is <math>\pi /T</math>. The | + | width at half maximum (in <math>\omega</math>-space) is <math>\pi /T</math>. |
| + | |||
| + | The | ||
central maximum can be made arbitrarily sharp simply by increasing | central maximum can be made arbitrarily sharp simply by increasing | ||
<math>T</math>. In fact, SOF can be used in this fashion to produce line | <math>T</math>. In fact, SOF can be used in this fashion to produce line | ||
| Line 115: | Line 120: | ||
variations, for instance due to fluctuations in an applied field, | variations, for instance due to fluctuations in an applied field, | ||
either in space or in time, are averaged out. | either in space or in time, are averaged out. | ||
| + | |||
* The Rabi method requires an applied oscillatory field having | * The Rabi method requires an applied oscillatory field having | ||
uniform phase: this is difficult to accomplish if the flight path | uniform phase: this is difficult to accomplish if the flight path | ||
is long compared to the wavelength. In contrast, the Ramsey | is long compared to the wavelength. In contrast, the Ramsey | ||
method requires only that the phase be constant across the short | method requires only that the phase be constant across the short | ||
| − | coils of length <math>\ell</math>. As we will see, this means that Doppler effects can be | + | coils of length <math>\ell</math>. As we will see, this means that Doppler effects can be to a large extent eliminated. |
| − | to a large extent eliminated. | + | |
* By the Rabi method the resonance linewidth due to a thermal | * By the Rabi method the resonance linewidth due to a thermal | ||
beam is 1.07 <math>\alpha /\ell</math>, whereas by the Ramsey method it is | beam is 1.07 <math>\alpha /\ell</math>, whereas by the Ramsey method it is | ||
only 0.65 <math>\alpha /\ell</math> The linewidth is reduced almost by a | only 0.65 <math>\alpha /\ell</math> The linewidth is reduced almost by a | ||
factor of two. | factor of two. | ||
| + | |||
* In the presence of radiative decay or some other loss | * In the presence of radiative decay or some other loss | ||
mechanism the Ramsey method can be used to selectively observe | mechanism the Ramsey method can be used to selectively observe | ||
| Line 131: | Line 138: | ||
resonance line which is narrower than the "natural" linewidth, | resonance line which is narrower than the "natural" linewidth, | ||
though one must pay a price in reduced signal intensity. | though one must pay a price in reduced signal intensity. | ||
| − | * Numerous experimental effects can be measured or reduced by | + | |
| − | modulating the relative phase of the two fields. | + | * Numerous experimental effects can be measured or reduced by modulating the relative phase of the two fields. |
| + | |||
* The method is not restricted to atomic beams: the important | * The method is not restricted to atomic beams: the important | ||
point is that the applied fields interfere in {\it time}. The | point is that the applied fields interfere in {\it time}. The | ||
method can be applied to a fixed sample by applying the fields in | method can be applied to a fixed sample by applying the fields in | ||
some desired sequence of pulses. | some desired sequence of pulses. | ||
| − | * The field-free region (or the free-evolution time <math>T</math>) can be used to | + | |
| − | enrich the experiment by having the atoms interact with some other system (such | + | * The field-free region (or the free-evolution time <math>T</math>) can be used to enrich the experiment by having the atoms interact with some other system (such as a cavity, c.f. the work of the Haroche group) and observing the resulting phase change to the interference pattern. |
| − | as a cavity, c.f. the work of the Haroche group) and observing the resulting | ||
| − | phase change to the interference pattern. | ||
Latest revision as of 03:00, 6 February 2009
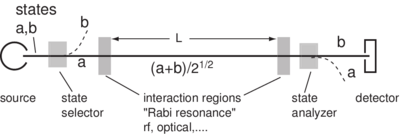
The separated oscillatory field (SOF) technique is one of the most powerful methods of precision spectroscopy. As the name suggests, it involves two sequential applications of the transition-producing field to the system under study with an interval in between. This technique was originally conceived by Norman Ramsey in 1948 for application in RF studies of molecular beams using two separated resonance coils through which the molecular beams passed sequentially. It represents the first deliberate exploitation of a quantum superposition state. Subsequently it has been extended to high frequencies where the RF regions were in the radiation zone (i.e. source-free), to two photon transitions, to rapidly decaying systems, and to experiments where the two regions were temporally (rather than spatially) separated. It is routinely used to push measurements to the highest possible precision (eg. in the Cs beam time standard apparatus). Ramsey shared the 1990 Nobel prize for inventing this method. Figure \ref{Ramsey-apparatus} shows a typical configuration. \begin{figure} \centering
\caption{ Separated oscillatory field atomic beam resonance. The two-state atom experiences a pulse in the first oscillatory field, and another pulse in the second field. In between, the atom moves freely for distance L. As viewed in the rotating frame, on resonance the second field will have the correct phase on resonance, no matter how long it takes the atom to traverse distance L. Off-resonance, however, a phase difference accumulates with the increasing time. As a result, when the frequency is slowly swept, an interference pattern is generated whose frequency width is , where v is the atom's velocity. }
\end{figure} The atomic beam resonance region is composed of two oscillatory field regions, each of length , separated by distance . The resonance pattern reveals an interference fringe structure with characteristic width / , where is the most probable velocity for a thermal distribution of atoms at temperature (see the figure below). Of course a single Rabi coil of the same length would produce approximately the same resonance width.
The transition probability for the Ramsey method can be calculated by straightforward application of the formalism presented earlier. Details are described in Reference \cite{Ramsey1956}, Section V.4.2. The result is that the transition probability for a two-state system is
where , and , where is the average energy separation of the two states along the path between the coil. and . The first line in this expression is just 4 times the probability of transition for a spin passing through one of the oscillating fields. All interference terms (which must involve ) are contained in the second term. The quantity is the phase difference accumulated by the spin in the field-free region relative to the oscillating field in the first region. If the phase in the second oscillating field region differs from the phase in the first region, the above results must be modified by adding the difference to in the above equations. \begin{figure} \centering
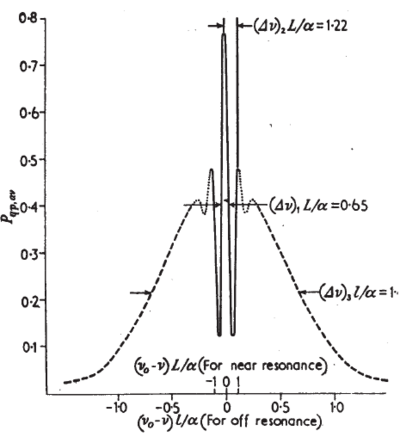
\caption{Transition probability by the separated oscillatory field method as a function of frequency. is the distance between the excitation regions; is the most probably velocity in the beam. Hence, is approximately the average time of the measuring process. The "Ramsey fringe" is shown by the solid line: it is superimposed on the "Rabi pedestal", dashed line, which is the resonance curve for a single oscillating field region. From Reference \cite{Ramsey1956}.}
\end{figure} The SOF technique is based on an interference between the excitations produced at two separated fields - thus it is sensitive to the phase difference (coherence) of the oscillating fields. The method is most easily understood by consideration of the classical spin undergoing magnetic resonance in SOF's. To maximize the interference between the two oscillating fields, we want there to be a probability of for a transition in each resonance region. This is achieved by adjusting both field intensities ( above) so that (an interaction with this property is termed a " pulse" if the system is at resonance, in which case the spin's orientation is now along in the rotating coordinate system).
During the field-free time , the spin precesses merrily about the constant field between the two oscillating-field regions. When it encounters the second oscillatory field, it receives a second interaction equal to the first. If the system is {\it exactly} on resonance, this second interaction will just complete the inversion of the spin. If, on the other hand, the system is off resonance just enough so that (but ) then the spin will have precessed about an angle less far than the oscillating field.
It will consequently lie in the - direction rather than in the direction in the coordinate system rotating with the second oscillatory field , and as a result the second field will precess the spin back to + , its original direction, and the probability of transition will be 0! A little more thought shows that the transition probability will oscillate sinusoidally with period . The central maximum of this interference pattern is centered at and its full width at half maximum (in -space) is .
The central maximum can be made arbitrarily sharp simply by increasing . In fact, SOF can be used in this fashion to produce line widths for decaying particles which are narrower than the reciprocal of the natural line width! (This does not violate the uncertainty principle because SOF is a way of selecting only those few particles which have lived for time .) The separated oscillatory field method (the "Ramsey method") has the following important properties compared to the single field method ("Rabi method").
- The resonance frequency depends on the {\it mean} energy
separation of the two states between the coils: instantaneous variations, for instance due to fluctuations in an applied field, either in space or in time, are averaged out.
- The Rabi method requires an applied oscillatory field having
uniform phase: this is difficult to accomplish if the flight path is long compared to the wavelength. In contrast, the Ramsey method requires only that the phase be constant across the short coils of length . As we will see, this means that Doppler effects can be to a large extent eliminated.
- By the Rabi method the resonance linewidth due to a thermal
beam is 1.07 , whereas by the Ramsey method it is only 0.65 The linewidth is reduced almost by a factor of two.
- In the presence of radiative decay or some other loss
mechanism the Ramsey method can be used to selectively observe long-lived atoms: atoms which have decayed are simply absent from the interference pattern. This makes it possible to observe a resonance line which is narrower than the "natural" linewidth, though one must pay a price in reduced signal intensity.
- Numerous experimental effects can be measured or reduced by modulating the relative phase of the two fields.
- The method is not restricted to atomic beams: the important
point is that the applied fields interfere in {\it time}. The method can be applied to a fixed sample by applying the fields in some desired sequence of pulses.
- The field-free region (or the free-evolution time ) can be used to enrich the experiment by having the atoms interact with some other system (such as a cavity, c.f. the work of the Haroche group) and observing the resulting phase change to the interference pattern.







![{\displaystyle {\begin{aligned}P=&4{\frac {\omega _{R}^{2}}{a^{2}}}\sin ^{2}(a\tau /2)\times \\&\left[\cos(\delta \omega T/2)\cos(a\tau /2)-\left({\frac {\omega -\omega _{0}}{a}}\right)\sin(\delta \omega T/2)\sin(a\tau /2)\right]^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe3e7fe74f504a7338854ea99646ab0d2b3af05a)