Difference between revisions of "Two-Photon Excitation"
imported>Wikibot m (New page: donewcmd error! no pattern match \newcommand{\QU}[1]{\par% \refstepcounter{question}\emph\thequestion: #1} = Two-Photon Excitation = == Introduction == Every radiative process described s...) |
imported>Wikibot m |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
== Introduction == | == Introduction == | ||
Every radiative process described so far has involved a single | Every radiative process described so far has involved a single | ||
| Line 51: | Line 47: | ||
\begin{figure} | \begin{figure} | ||
\centering | \centering | ||
| − | ::[[Image:Two-Photon_Excitation-two-photon-levels|thumb|408px|none|]] | + | ::[[Image:Two-Photon_Excitation-two-photon-levels.png|thumb|408px|none|]] |
\caption{Two-photon absorption} | \caption{Two-photon absorption} | ||
| Line 245: | Line 241: | ||
\begin{figure} | \begin{figure} | ||
\centering | \centering | ||
| − | ::[[Image:Two-Photon_Excitation-Raman|thumb|408px|none|]] | + | ::[[Image:Two-Photon_Excitation-Raman.png|thumb|408px|none|]] |
\caption{Raman emission. Photon <math>\omega_2</math> can be emitted | \caption{Raman emission. Photon <math>\omega_2</math> can be emitted | ||
spontaneously, or by stimulated emission. } | spontaneously, or by stimulated emission. } | ||
| Line 345: | Line 341: | ||
)^2} \\ | )^2} \\ | ||
&=& \frac{2}{\pi} \frac{(\gamma /2 )}{(\gamma /2 )^2 + (\omega_0 - | &=& \frac{2}{\pi} \frac{(\gamma /2 )}{(\gamma /2 )^2 + (\omega_0 - | ||
| − | \omega_1 - \omega_2 + (k_1 + k_2 )\ | + | \omega_1 - \omega_2 + (k_1 + k_2 )\cdot v )^2} . |
\end{array}</math> | \end{array}</math> | ||
| Line 370: | Line 366: | ||
\begin{figure} | \begin{figure} | ||
\centering | \centering | ||
| − | ::[[Image:Two-Photon_Excitation-pedestal|thumb|408px|none|]] | + | ::[[Image:Two-Photon_Excitation-pedestal.png|thumb|408px|none|]] |
\caption{Two-photon doppler-free spectrum. A narrow peak due to the process | \caption{Two-photon doppler-free spectrum. A narrow peak due to the process | ||
involving two photons from counterpropagating beams sits atop a broad pedestal | involving two photons from counterpropagating beams sits atop a broad pedestal | ||
Revision as of 14:04, 5 February 2009
Contents
Introduction
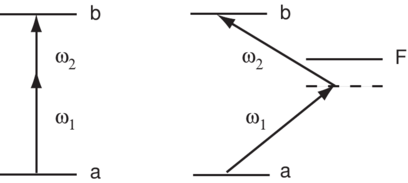
Every radiative process described so far has involved a single photon, whether it be a hyperfine transition in magnetic resonance, optical excitation, or spontaneous emission. However, at higher power, when first-order perturbation theory breaks down, processes can occur in which an atom {\it simultaneously} absorbs two or more photons. Such multi-photon processes can lead to ionization of atoms or dissociation of molecules in intense laser fields, and phenomena such as free-to-free transitions in which an electron absorbs successive quanta as it flies out from the field of an atom. Two-photon processes have become one of the standard tools in atomic physics for exciting atoms to states whose energies are too high to achieve with a single photon (e.g. Rydberg states) and also to states of the same parity that would normally be inaccessible. In addition, a number of ultra-high resolution (doppler-free) spectroscopic techniques are based on two-photon processes. The ubiquitous phenomena of resonance fluorescence and Rayleigh scattering are also two-photon processes. Our approach will be to use second-order perturbation theory, extending the first order development used in earlier chapters in a straightforward fashion. An alternative approach involves solving the dynamical equations in the same manner as we analyzed the two-level system. However, the perturbation approach is appropriate in many cases, and is simpler than the dynamical approach. The aim is to cause a transition Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a \rightarrow b} by applying two fields:
where
States Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a \rangle} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |b \rangle } have the same parity, so a single photon transition is forbidden. The process is shown in Fig.~\ref{fig:two-photon}, left. A more realistic view is shown in
Fig.~\ref{fig:two-photon} right, where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f \rangle}
represents some
intermediate state of
opposite parity. One way to describe the process is that photon Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_1} causes a transition from to a "virtual" state near Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f \rangle} and the second photon at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2} carries the system from the virtual state to the final state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |b \rangle} . The interpretation of the virtual state will be discussed in Section \ref{sec:virtual}. Note that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f \rangle} , in reality, represents one of a complete set of eigenstates which have non-vanishing dipole matrix elements with . \begin{figure} \centering
\caption{Two-photon absorption}
\end{figure}
Calculation of the Two-Photon Rate
The Hamiltonian is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = - {\vec {\mathcal{E}}} \cdot d} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d =-e r} . With the field described by Eq.\ \ref{eq:introone}, we have
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = - \frac{1}{2} {\left( e^{i\omega_1 t} + e^{-i\omega_1 t}\right)} {\mathcal{E}}_1 \hat{e}_1 \cdot d - \frac{1}{2} {\left( e^{i\omega_2 t} + e^{-i\omega_2 t}\right)} {\mathcal{E}}_2 \hat{e}_2 \cdot d . }
Defining
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{fa,1} = - E_1 \langle f| \hat{e}_1 \cdot d| a \rangle , ~~~ H_{fa,2} = - E_2 \langle f | \hat{e}_2 \cdot d| a \rangle , }
the matrix element is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{fa} = \frac{H_{fa,1}}{2} e^{-i\omega_1 t} + \frac{H_{fa,2}}{2} e^{-i\omega_2 t} . }
As the counterrotating terms are usually negligible, we have dropped them for simplicity. Following the procedure used earlier, the first order solution for the amplitude Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_f} of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle | f \rangle} is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_f^{[1]} = \frac{1}{2i\hbar} \int_0^t {\left[ H_{fa,1} e^{-i(\omega_1 -\omega_{fa} )t^\prime} + H_{fa,2} e^{-i(\omega_2 - \omega_{fa} )t^\prime} dt^\prime \right]} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2\hbar} {\left[ \frac{H_{fa,1} (e^{-i(\omega_1 - \omega_{fa} ) t} - 1)}{\omega_1 - \omega_{fa} } + \frac{H_{fa,2} (e^{-i(\omega_2 - \omega_{ fa} ) t} - 1)}{\omega_2 - \omega_{fa} } \right]} . }
The second order solution for the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} state amplitude, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_b^{[2]}} , is found from
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \dot{a}_b^{[2]} = \sum_{k} H_{bk} a_k^{[1]} e^{i\omega_{bk}. t} }
The contribution to the sum due to state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_b^{[2]} = \frac{1}{i\hbar} \int_0^t \langle b| H | f \rangle e^{i\omega_{bf} t^\prime} a_f^{[1]} (t^\prime ) dt^\prime. }
Introducing
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{bf,1} = -{\mathcal{E}}E_1 \langle b | \hat{e}_1 \cdot d | f \rangle , ~~~ H_{bf,2} = - {\mathcal{E}}_2 \langle b | \hat{e}_2 \cdot d | f \rangle }
and defining Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0 \equiv \omega_{ba}} , we have,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle b | H | f \rangle = \frac{H_{bf,1} }{2} e^{-i\omega_1 t} + \frac{H_{bf,2}}{2} e^{-i\omega_2 t} . }
\noindent Eq.\ \ref{eq:ctprsix} yields
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} a_b^{[2]} &=& \frac{1}{4\hbar^2} \sum_{f} \left[ \frac{H_{bf,1} H_{fa,1}}{\omega_1 - \omega_{fa}} \frac{e^{i(\omega_0 - 2 \omega_1 )t} -1}{\omega_0 - 2\omega_1} + \frac{H_{bf,2} H_{fa,2}}{\omega_2 - \omega_{fa}} \frac{e^{i(\omega_0 - \omega_2 ) t} -1}{\omega_0 - 2\omega_2} \right. \\ & &+ \left. \frac{H_{bf,2} H_{fa,1}}{\omega_1 - \omega_{fa} } \frac{e^{i (\omega_0 - \omega_1 - \omega_2)t} -1}{\omega_0 - \omega_1 - \omega_2} + \frac{H_{bf,1} H_{fa,2}}{\omega_2 - \omega_{fa}} \frac{e^{i (\omega_0 - \omega_1 - \omega_2 ) t} -1}{\omega_0 - \omega_1 - \omega_2} \right] . \end{array}}
Note that the first two terms involve absorbing two photons from the same beam, while the last two involve absorbing one photon from each of the two beams. When two different frequencies are used, the first terms are invariably far from resonance and can be neglected. In the case of absorbing two photons at the same frequency, discussed below, all four terms contribute. \section{Two-photon rate with a single intermediate state} Suppose that is close to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{ka}} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is a particular intermediate state. In this case Eq.\ \ref{eq:ctprnine} becomes
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_b^{[2]} \approx \frac{1}{4\hbar^2} \frac{H_{bk,2} H_{ka,1} }{\omega_1 - \omega_{ka}} \frac{e^{i(\omega_0 - \omega_1 - \omega_2 ) t} -1}{\omega_1 - \omega_1 - \omega_2}. }
We then obtain for the transition probability
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{a\rightarrow b}^{[2]} = \frac{1}{{\left(4\hbar^2\right)^2}} \frac{ | H_{bk,2} |^2| H_{ka,1} |^2}{(\omega_1 - \omega_{ka} )^2} \frac{\sin^2\left[ ( \omega_0 - \omega_1 - \omega_2 ) t/2\right]}{[(\omega_0 - \omega_1 - \omega_2 )/2]^2}. }
Recalling that
we obtain
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{ab}^{(2)} = \frac{\pi}{8\hbar^4} \frac{| H_{bk,2} |^2 | H_{ka,1} |^2}{(\omega_1 - \omega_{ka} )^2}\delta(\omega_0-\omega_1-\omega_2). }
Integrating over the appropriate spectral distribution gives
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{ab}^{(2)} = \frac{\pi}{8\hbar^4} \frac{| H_{bk,2} |^2 | H_{ka,1} |^2}{(\omega_1 - \omega_{ka} )^2} f(\omega_0 ). }
We can cast the transition rate into a more familiar form by introducing the usual Rabi frequencies
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_R^{(1)} = \frac{| H_{ka,1} | }{\hbar}, ~~\omega_R^{(2)} = \frac{| H_{ka,2} | }{\hbar}. }
Denoting the detuning of the intermediate state by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \equiv \omega_1 - \omega_{ka}, }
we can define the two-photon Rabi frequency by
and we have
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{ab} = \frac{\pi}{2} \omega_{R2}^2\delta(\omega_0-\omega_1-\omega_2) , }
in analogy with the expression for one-photon transitions. A more useful expression for the two-photon transition rate is in terms of the radiation intensity, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} . Noting that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal{E}}^2 =8\pi I/c} (cgs units), we have from Eq.\ \ref{eq:ctprtwo}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle | H_{ka,1} |^2 = {\mathcal{E}}^2_1 | \langle k| \hat{e}_1 \cdot d | a \rangle |^2 = 8\pi | d_{ka}^{(1)} |^2 I_1 /c , }
Eq.\ \ref{eq:ctpathree} becomes
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{ab}^{(2)} = \frac{8\pi^3}{\hbar^4 c^2} \frac{| D_{ka}^{(2)} |^2 | D_{bk}^{(2)} |^2}{\Delta^2 } f (\omega_0 ) I_1 I_2 . }
In the case where both photons emanate from a single laser beam, equation \ref{eq:ctpasix} further simplifies to
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{R2}=\frac{|\omega_R^{(1)}|^2}{2\Delta}. }
Discussion
Applicability of one-photon results
The definition above of a two-photon Rabi frequency suggests an analogy between two-photon and one-photon transitions. The analogy is a powerful one, as many results from the study of one-photon transitions carry over to the two-photon case. These include \begin{itemize} \item{Lineshape: if the rate of spontaneous two-photon emission from to is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} , then the transition has Lorentzian lineshape
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\Delta \omega) = \frac{2}{\pi} \frac{\gamma/2}{(\delta\omega)^2+\gamma^2/4}, }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta\omega=\omega_0-2\omega} is the two-photon detuning.} \item{Saturation: like single-photon transitions, two-photon transitions saturate as the rate of excitation approaches half the natural linewidth. By analogy with the one-photon case, one can define a two-photon saturation parameter Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_2=2\omega_{R2}^2/\gamma^2} .} \item{Spontaneous emission: In calculating the rate of emission, we still have , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\in\{1,2\}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i} is the number of photons in the mode of frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_i} ; the two-photon emission rate thus scales as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |E_1|^2 |E_2|^2\propto (n_1+1)(n_2+1)} , where for every emission events in which both photons are stimulated, there is one event in which both photons are spontaneous, and there are Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i} events in which the photon in mode Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} is stimulated and the other is spontaneous. The rate of absorption is the same as the rate of doubly-stimulated emission.} \item{The two-photon transition rate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{ab}} looks similar to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{kb}^\mathrm{1-ph, 2}} (the rate of one-photon emission at frequency ), but is diminished by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[\frac{\omega_R^{(1)}}{2\Delta}\right]^2} , the squared amplitude of state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |k\rangle} admixed into state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a\rangle} .} \item{Two-photon emission: Consider the case where the population is initially in state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |b\rangle} , but there is only one laser, and its frequency is close to the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\rightarrow b} transition. Then the two photon emission rate is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{ba}^\mathrm{2-ph} = \Gamma_{ka}\left[\frac{H_{kb,1}}{2\Delta}\right]^2, }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{ka}} is the rate of spontaneous emission from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |k\rangle} to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a\rangle} and is the admixture of state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |k\rangle} into the initial state. This admixture may also be regarded as the "population of the virtual state." } \end{itemize}
What is the virtual state?
In calculating rates of two-photon processes, we have been making use of a "virtual" state near some intermediate state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f\rangle} with one-photon couplings to both the initial state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a\rangle} and the final state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |b\rangle} . We have also noted that, more generally, the virtual state can be a superposition of several states---but \textit{all} at the frequency of the drive. We can think of the virtual state purely mathematically as the thing that appears in the perturbation sum. But does it have a physical interpretation? To what extent does the transition from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a\rangle} to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |b\rangle} occur \textit{via} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f\rangle} ? And how can Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f\rangle} serve as an intermediate state given that the transitions into and out of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f\rangle} apparently do not conserve energy? One interpretation is in the dressed atom picture (covered in 8.422). Because of the couplings introduced by the laser field, the true eigenstates of the system are not Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a\rangle} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |b\rangle} , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f\rangle} but the so-called "dressed states." If we start with the system in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a\rangle} and adiabatically turn on the field coupling Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a\rangle} to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f\rangle} , the system will evolve into the dressed state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a'\rangle \approx |a\rangle+\frac{\omega_R^{(1)}}{2\Delta}|f\rangle} . As we have seen above and will see again in the case of spontaneous Raman scattering, the rates of two-photon processes can often be understood in terms of this admixture of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f\rangle} into Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a\rangle} , the "population of the virtual state" Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{\omega_R}{2\Delta}\right)^2} . Thus, one can interpret the virtual state as a component of the dressed atom wavefunction. Another way to understand the virtual state is to consider the lifetime of the atom in the intermediate state. Consider the case of two-photon emission from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |b\rangle} to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a\rangle} via Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f\rangle} . Although a transition from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |b\rangle} to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f\rangle} violates energy conservation by an amount Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} , the Heisenberg uncertainty principle allows the atom to remain in the intermediate state for a time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar/\Delta} . And indeed, if one observes the emitted photons, one finds that the two photons are correlated in time to within .
Raman Processes
Stimulated Raman scattering
We have considered two-photon absorption processes, but stimulated emission can also occur as can be seen from Fig.~\ref{fig:two-photon}. \begin{figure} \centering
\caption{Raman emission. Photon Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2} can be emitted spontaneously, or by stimulated emission. }
\end{figure} In this case, the transition Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\rightarrow b} occurs by absorbing a photon at frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_1} , and emitting a photon at frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2} . If the transition is stimulated by two applied radiation fields, then the process is known as stimulated Raman scattering. If , the emission is called Stokes radiation. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2 > \omega_1} , the emission is called anti-Stokes radiation. In either case, the frequencies are related by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_1 = \omega_2 + \omega_{ba} . }
Our treatment of the two-photon transition applies, except that one interaction step corresponds to emission, rather than absorption. The change is trivial: the counter-rotating term at frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \omega_2} in Eq.\ \ref{eq:ctprone}, which was dropped, is retained and the rotating term, at frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2} , is dropped in its place. This merely changes the sign of in the ensuing steps, so we again obtain
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{ab}^\mathrm{Raman}=\frac{\pi}{2}\omega_{R2}^2\delta(\Delta\omega), }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{R2}=\frac{\omega_R^{(1)}\omega_R^{(2)}}{2\Delta}} as before, but in this case
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\omega = \omega_0-\omega_1+\omega_2. }
Spontaneous Raman scattering
An important aspect of Raman scattering that differentiates it from two-photon absorption is that the emission of the photon at frequency Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2} can be spontaneous. Spontaneous emission is generally too slow to be useful at low frequencies but in the optical regime the spontaneous rate can be large enough to cause a sizeable scattering signal. Initially, spontaneous Raman scattering was the only important process: not until the advent of the laser did stimulated Raman scattering became useful. We can estimate the rate of spontaneous Raman scattering by considering absorption at and emission at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2} as separate processes, though strictly speaking only one process is involved. We start by evaluating the spontaneous emission at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2} . This takes place from a virtual intermediate state, which we shall denote as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} . The spontaneous emission rate is given by the familiar expression
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{fb} = \frac{4}{3} \alpha^3 \omega_2^3 | \langle f | r | b \rangle |^2. }
Next, we consider the problem of "populating" the virtual state. The rate of exciting the state can be expressed in terms of the Rabi frequency
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_R = {\mathcal{E}}_1 | \langle f | \hat{e}_1 \cdot d | a \rangle | /\hbar }
The detuning from state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta =\omega_1 -\omega_{fa}} . The transition rate to the intermediate state is approximately
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{af}\approx \frac{\omega_R^2}{\Delta} }
The time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} the atom can occupy the state, however, is limited by the uncertainty principle to . Hence the probability that state Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} is occupied is roughly Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{af}\; \tau \sim \omega_R^2/\Delta^2} . Using either perturbration theory or the dressed atom picture, one can solve for the virtual state population with the correct numerical factor: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_R^2/(4\Delta^2)} . Putting the above together, we obtain the rate for spontaneous Raman scattering from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} to :
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{ab}^{sr} = \frac{\omega_R^2}{4\Delta^2}\cdot A_{fb} . }
Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_R^2 \sim E^2 \sim I} , the spontaneous Raman rate depends linearly on the power. The absorption process can be continued, allowing multi-photon Raman transitions to a final state. Note that even if a = b (i.e., if the internal state of the atom is unchanged by the two-photon transition), the final state differs from the initial state by one photon recoil. Hence, resonant fluorescence and Rayleigh scattering are Raman processes!
Two-photon Doppler-free spectroscopy
The Doppler effect is the most common source of inhomogeneous line broadening. (Inhomogeneous broadening occurs because the resonance frequencies of different atoms are shifted by different amounts, giving a width to the ensemble. This is in contrast to homogeneous broadening, when the response of each atom is the same, as in the case of spontaneous decay.) If two-photon excitation involves absorption from two light beams with frequencies and wave vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\omega_1 , \omega_2 )} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ( {\bf k}_1 , k_2 )} , respectively, where , then the frequencies "seen" by an atom moving with velocity v are, to first order in v/c,\\
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_1^\prime = \omega_1 - k_1 \cdot v, ~~~~ \omega_2^\prime = \omega_2 - k_2 \cdot v. }
The line shape function for an atom moving with velocity v is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} f ( \omega_1 , \omega_2 ) &=& \frac{2}{\pi} \frac{(\gamma /2 )}{(\gamma /2)^2 + (\omega_0 - \omega_1^\prime - \omega^\prime_2 )^2} \\ &=& \frac{2}{\pi} \frac{(\gamma /2 )}{(\gamma /2 )^2 + (\omega_0 - \omega_1 - \omega_2 + (k_1 + k_2 )\cdot v )^2} . \end{array}}
The Doppler effect is minimized by taking Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{k}_1 = - \hat{k}_2} , in which case the shift is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \omega_D = (\omega_1 - \omega_2 ) v/c . }
The ensemble line shape function is obtained by averaging over the distribution of velocities. Clearly, it is desirable to use frequencies as similar as possible. The ideal case is when , which would occur in two photon-absorption from counter-propagating beams from the same laser. The simplest way to assure counter-propagating beams is to use a standing wave. Consequently, two-photon absorption in a standing wave displays no first-order Doppler broadening. Nevertheless, there is a residual second-order Doppler broadening. The second-order Doppler shift is given by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta\omega_{D2}}{\omega} = - \frac{1}{2} \frac{v^2}{c^2} = - \frac{Mv^2/2}{Mc^2} . }
\begin{figure} \centering
\caption{Two-photon doppler-free spectrum. A narrow peak due to the process involving two photons from counterpropagating beams sits atop a broad pedestal due to that involving pairs of photons from the same beam.}
\end{figure} Taking Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} M \overline{v^2} \simeq k_B T} , we have
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta \omega_{D2} }{\omega} \approx \frac{-k_BT}{Mc^2} . }
At room temperature, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B T = (1/40)} eV. For hydrogen, GeV . Consequently, the fractional second order Doppler shift is about Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\times 10^{-11}} . If one considers spectroscopy at a resolution of 1 part in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{13}} or better, the second order Doppler shift can be a major source of systematic error. Fortunately, methods have been developed for cooling below a millikelvin, where the effect is unimportant, at least for the next few years. Also, in heavier atoms, the second order Doppler effect is correspondingly diminished. A particularly important case is two-photon absorption on the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1S \rightarrow 2S} transition in hydrogen. The 2S state is metastable and has a lifetime of 1/7 sec, yielding an extremely high Q for the transition and the possibility of ultra-high spectral resolution. The excitation operator has been calculated for hydrogen by \cite{Bassani1977}. The result yields
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{1s,2s} = 84 \frac{I^2}{\gamma} s^{-1} }
where the intensity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} is now expressed in WFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot {\rm cm}^{-2}} . A transition becomes saturated when the transition rate equals half the linewidth, or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{1s,2s} = \gamma/2} . The required power is only 0.6 WFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle /{\rm cm}^2} . By using two-photon Doppler-free excitation in hydrogen, H\"{a}nsch and his group have been able to achieve an experimental linewidth below 10 kHz \cite{Niering2000}. The linewidth is dominated by the time of flight of the atoms across the laser beam. Although the experimental linewidth of several kHz may seem large compared to the natural linewidth of 1 Hz, it is impressively narrow considering that the spectral linewidth was many MHz not many years ago. \putbib





![{\displaystyle {\frac {\sin ^{2}\left[(\omega _{0}-\omega _{1}-\omega _{2})t/2\right]}{[(\omega _{0}-\omega _{1}-\omega _{2})/2]^{2}}}{\xrightarrow[{t\rightarrow \infty }]{}}2\pi t\delta (\omega _{0}-\omega _{1}-\omega _{2}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec23f6a89d79292a7a49e6172bab1c7a609c3c5d)






![{\displaystyle \left[{\frac {H_{kb,1}}{2\Delta }}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5045eed055ce2e320e71329782faab296e3f4959)








