Interferometer Heisenberg limit

The shot noise limit is not fundamental. Here is a simple argument that something better should be possible. Recall that the desired signal at the output of our Mach-Zehnder interferometer is $X=a^{\dagger }a-b^{\dagger }b$, and the noise is $Y=a^{\dagger }b+b^{\dagger }a$. If the inputs have $a^{\dagger }a=n$ and $b^{\dagger }b=0$, and if $Y$ were zero, then the measured signal would be $n\cos \phi$. And at the balanced operating point $\phi =\pi /2$,

${\frac {|\Delta m|}{\Delta \phi }}=n\sin \phi \leq n\,.$

Thus, if the smallest photon number change resolvable is $\Delta m=1$, then $n\Delta \phi \geq 1$, from which it follows that

$\Delta \phi \geq {\frac {1}{n}}\,.$

This is known as the "Heisenberg limit" on interferometry. There are some general proofs in the literature that such a limit is the best possible on interferometry. It governs more than just measurements of phase shifters; gyroscopes, mass measurements, and displacement measurements all use interferometers, and obey a Heisenberg limit.

The argument above only outlines a sketch for why $1/n$ might be an achievable limt, versus $1/{\sqrt {n}}$; it assumes that the noise $Y$ can be made zero, however, and does not provide a means for accomplishing this in practice. Many ways to reach the Heisenberg limit in interferometry are now known. Given the basic structure of a Mach-Zehnder interferometer,

one can consider changing the input state $|\psi _{in}{\rangle }$, changing the beamsplitters, or changing the measurement.

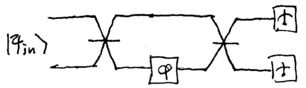
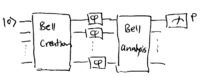
Common to all of these approaches is the use of entangled states. How entanglement makes Heisenber-limited interferometry possible can be demonstrated by the following setup. Let us replace the beamsplitters in the Mach-Zehnder interferometer with entangling and dis-entangling devices:

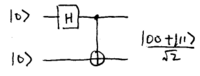
Conceptually, the unusual beamsplitters may be the nonlinear Mach-Zehnder interferometers we discussed in Section~2.3. They may also be described by simple quantum circuits, using the Hadamard and controlled-{\sc not} gate; for two qubits, the circuit is

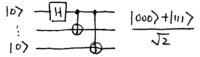
Note how the output is one of the Bell states. For three qubits, the circuit is

This output state, $|000{\rangle }+|111{\rangle }$ (suppressing normalization) is known as a GHZ (Greenberger-Horne-Zeilinger) state. Straightforward generalization leads to larger "Schrodinger cat" states $|00\cdots 0{\rangle }+|11\cdots 1{\rangle }$, using one Hadamard gate and $n$ controlled-{\sc not} gates. Note that the reversed circuit unentangles the cat states to produce computational basis states.

The important feature of such $n$-qubit cat states, for our purpose, is how they are transformed by phase shifters. A single qubit $|0{\rangle }+|1{\rangle }$ becomes $|0{\rangle }+e^{i\phi }|1{\rangle }$. Similarly, two entangled qubits in the state $|00{\rangle }+|11{\rangle }$, when sent through two phase shifters, becomes $|00{\rangle }+e^{2i\phi }|11{\rangle }$, since the phases add. And $n$ qubits in the state $|00\cdots 0{\rangle }+|11\cdots 1{\rangle }$ sent through $n$ phase shifters becomes $|00\cdots 0{\rangle }+e^{ni\phi }|11\cdots 1{\rangle }$.

When such a phase shifted state is un-entangled, using the reverse of the entangling circuit, the $n$ controlled-{\sc not} gates leave the state $|00\cdots 0{\rangle }[|0\rangle +e^{ni\phi }|1\rangle ]$, where the last $n-1$ qubits are left in $|0{\rangle }$, and the first qubit (the qubit used as the control for the {\sc cnot} gates) is

${\frac {|0\rangle +e^{ni\phi }|1{\rangle }}{\sqrt {2}}}\,.$

Compare this state with that obtained from the single qubit interferometer, Eq.(\ref{eq:l7-1qubitphase}); instead of a phase $\phi$, the qubit now carries the phase $n\phi$. This means that the probability $P$ of measuring a single photon at the output becomes

$P={\frac {1+\cos(n\phi )}{2}}\,.$

The standard deviation, from repeating this experiment, on average, would be

$\Delta P={\sqrt {P(1-P)}}={\frac {\sin(n\phi )}{2}}\,.$

Using $dP/d\phi =-n\sin(n\phi )/2$, we obtain for the uncertainty in $\phi$,

$\Delta \phi ={\frac {\Delta \phi }{\left|{\frac {dP}{d\phi }}\right|}}={\frac {1}{n}}\,,$

which meets the Heisenberg limit.