Interferometer Heisenberg limit

The shot noise limit is not fundamental. Here is a simple argument that something better should be possible. Recall that the desired signal at the output of our Mach-Zehnder interferometer is $X=a^{\dagger }a-b^{\dagger }b$, and the noise is $Y=a^{\dagger }b+b^{\dagger }a$. If the inputs have $a^{\dagger }a=n$ and $b^{\dagger }b=0$, and if $Y$ were zero, then the measured signal would be $n\cos \phi$. And at the balanced operating point $\phi =\pi /2$,

$\left|{\frac {\Delta M}{\Delta \phi }}\right|=n\sin \phi \leq n\,.$

Thus, if the smallest photon number change resolvable is $\Delta M=1$, then $n\Delta \phi \geq 1$, from which it follows that

$\Delta \phi \geq {\frac {1}{n}}\,.$

This is known as the "Heisenberg limit" on interferometry. There are some general proofs in the literature that such a limit is the best possible on interferometry. It governs more than just measurements of phase shifters; gyroscopes, mass measurements, and displacement measurements all use interferometers, and obey a Heisenberg limit.

Heisenberg limited interferometry with entangled states

The argument above only outlines a sketch for why $1/n$ might be an achievable limt, versus $1/{\sqrt {n}}$; it assumes that the noise $Y$ can be made zero, however, and does not provide a means for accomplishing this in practice. Many ways to reach the Heisenberg limit in interferometry are now known. Given the basic structure of a Mach-Zehnder interferometer,

one can consider changing the input state $|\psi _{in}{\rangle }$, changing the beamsplitters, or changing the measurement.

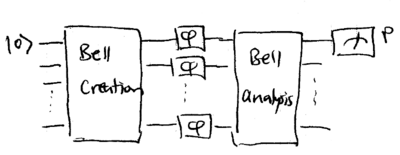
Common to all of these approaches is the use of entangled states. How entanglement makes Heisenber-limited interferometry possible can be demonstrated by the following setup. Let us replace the beamsplitters in the Mach-Zehnder interferometer with entangling and dis-entangling devices:

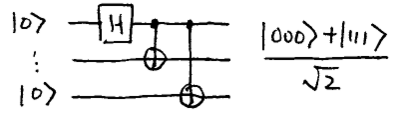
Conceptually, the unusual beamsplitters may be the nonlinear Mach-Zehnder interferometers we discussed in Section~2.3. They may also be described by simple quantum circuits, using the Hadamard and controlled-{\sc not} gate; for two qubits, the circuit is

Note how the output is one of the Bell states. For three qubits, the circuit is

This output state, $|000{\rangle }+|111{\rangle }$ (suppressing normalization) is known as a GHZ (Greenberger-Horne-Zeilinger) state. Straightforward generalization leads to larger "Schrodinger cat" states $|00\cdots 0{\rangle }+|11\cdots 1{\rangle }$, using one Hadamard gate and $n$ controlled-{\sc not} gates. Note that the reversed circuit unentangles the cat states to produce computational basis states.

The important feature of such $n$-qubit cat states, for our purpose, is how they are transformed by phase shifters. A single qubit $|0{\rangle }+|1{\rangle }$ becomes $|0{\rangle }+e^{i\phi }|1{\rangle }$. Similarly, two entangled qubits in the state $|00{\rangle }+|11{\rangle }$, when sent through two phase shifters, becomes $|00{\rangle }+e^{2i\phi }|11{\rangle }$, since the phases add. And $n$ qubits in the state $|00\cdots 0{\rangle }+|11\cdots 1{\rangle }$ sent through $n$ phase shifters becomes $|00\cdots 0{\rangle }+e^{ni\phi }|11\cdots 1{\rangle }$.

When such a phase shifted state is un-entangled, using the reverse of the entangling circuit, the $n$ controlled-{\sc not} gates leave the state $|00\cdots 0{\rangle }[|0\rangle +e^{ni\phi }|1\rangle ]$, where the last $n-1$ qubits are left in $|0{\rangle }$, and the first qubit (the qubit used as the control for the {\sc cnot} gates) is

${\frac {|0\rangle +e^{ni\phi }|1{\rangle }}{\sqrt {2}}}\,.$

Compare this state with that obtained from the single qubit interferometer, Eq.(\ref{eq:l7-1qubitphase}); instead of a phase $\phi$, the qubit now carries the phase $n\phi$. This means that the probability $P$ of measuring a single photon at the output becomes

$P={\frac {1+\cos(n\phi )}{2}}\,.$

The standard deviation, from repeating this experiment, on average, would be

$\Delta P={\sqrt {P(1-P)}}={\frac {\sin(n\phi )}{2}}\,.$

Using $dP/d\phi =-n\sin(n\phi )/2$, we obtain for the uncertainty in $\phi$,

$\Delta \phi ={\frac {\Delta \phi }{\left|{\frac {dP}{d\phi }}\right|}}={\frac {1}{n}}\,,$

which meets the Heisenberg limit.

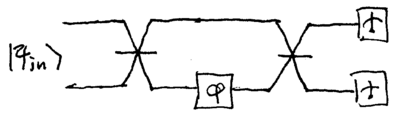
Heisenberg limited interferometry with "super beamsplitters"

Another way to reach the Heisenberg limit in an interferometer is with a different kind of beamsplitter. Suppose that instead of the usual beamsplitter, we have one which keeps $n$ photon states together, such that an input $|n,0\rangle$ is transformed to

${\frac {|n,0\rangle +|0,n\rangle }{\sqrt {2}}}$

With such an interferometer, then, an interferometer made with two such beamsplitters:

will provide a phase shift Failed to parse (unknown function "\n"): {\displaystyle e^{i\n\phi}} of angle proportional to $n$. The probability of measuring the output photon number to be zero is then

$P_{0}=\cos ^{2}(n\phi /2)$

which gives, much as in the entangled photon interferometer case,

${\sqrt {\langle \Delta P_{0}^{2}\rangle }}={\sqrt {P_{0}(1-P_{0})}}={\frac {\sin(n\phi )}{2}}$

Combining this with

$\left|{\frac {\partial P_{0}}{\partial \phi }}\right|={\frac {n\sin(n\phi )}{2}}$

gives

$\langle \Delta \phi \rangle ={\frac {\sqrt {\langle \Delta P_{0}^{2}\rangle }}{\left|{\frac {\partial P_{0}}{\partial \phi }}\right|}}={\frac {1}{n}}$

The ${\frac {|n,0\rangle +|0,n\rangle }{\sqrt {2}}}$ states have been called "high noon" states in the literature. In practice, the degree of optical nonlinearity required to create such states is largely impractical at optical wavelengths, at realistic degrees of loss. Howver, one method for realizing a "super beamsplitter" close to that imagined here has been proposed, for microwave photons. See <refbase>789</refbase>, and references therein.