Difference between revisions of "Squeezed light interferometry"
imported>Ichuang |
imported>Agrier |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
Heisenberg-limited interferometry can also be accomplished using a | Heisenberg-limited interferometry can also be accomplished using a | ||
variety of states of light, including [[Non-classical_states_of_light|squeezed states]] we studied earlier. Let us explore three configurations here. | variety of states of light, including [[Non-classical_states_of_light|squeezed states]] we studied earlier. Let us explore three configurations here. | ||
| − | Vacuum squeezed state input | + | |
| + | ==== Vacuum squeezed state input ==== | ||
| + | |||
| + | Because squeezed states can move | ||
noise between the <math>x</math> and <math>p</math> quadratures, it is intuitively | noise between the <math>x</math> and <math>p</math> quadratures, it is intuitively | ||
reasonable that a state with low phase noise could be used to provide | reasonable that a state with low phase noise could be used to provide | ||
| Line 88: | Line 91: | ||
\langle X \rangle &=& 0 | \langle X \rangle &=& 0 | ||
\\ | \\ | ||
| − | \langle X^2 \rangle &=& \langle n_a^2 - 2n_an_b + n_b^2 \rangle = | + | \langle X^2 \rangle &=& \langle n_a^2 - 2n_an_b + n_b^2 \rangle = 1 |
\,. | \,. | ||
\end{array}</math> | \end{array}</math> | ||
Thus, the uncertainty in <math>\phi</math> is | Thus, the uncertainty in <math>\phi</math> is | ||
:<math> | :<math> | ||
| − | {\langle}\Delta\phi \rangle = \frac{ | + | {\langle}\Delta\phi \rangle = \frac{1}{n} |
\,, | \,, | ||
</math> | </math> | ||
| − | which is | + | which is the Heisenberg limit. |
==== Yurke state: Experiment? ==== | ==== Yurke state: Experiment? ==== | ||
| Line 121: | Line 124: | ||
is | is | ||
:<math> | :<math> | ||
| − | |\psi \rangle = \frac{|n-1{\rangle}|n \rangle + \sqrt{n}|n{\rangle}|n-1{\rangle}}{\sqrt{2}} | + | |\psi \rangle = \frac{\sqrt{n} |n-1{\rangle}|n \rangle + \sqrt{n}|n{\rangle}|n-1{\rangle}}{\sqrt{2}} |
\,. | \,. | ||
</math> | </math> | ||
Latest revision as of 20:00, 25 February 2009
Heisenberg-limited interferometry can also be accomplished using a variety of states of light, including squeezed states we studied earlier. Let us explore three configurations here.
Vacuum squeezed state input
Because squeezed states can move noise between the and quadratures, it is intuitively reasonable that a state with low phase noise could be used to provide more accurate measurements of than is possible with a coherent state, which has equal noise in the two quadratures.
It might seem counter-intuitive, however, that we can get to the Heisenberg limit by replacing not the coherent state input, but rather, the vacuum state, in the Mach-Zehnder interferometer. This works because at the balanced operating point, the noise in the output is due to fluctuations entering in at the vacuum port. Before, we used as input. Let us now replace this by
where is a squeezed vacuum state. Recall that for the balanced interferometer, the final uncertainty in the phase measurement is
where , and . For the squeezed vacuum + coherent state input, we find
Thus, the uncertainty in the phase measurement is approximately
In the limit of large squeezing, ie , the squeezed vacuum has nonzero average photon number, , so this expression does not vanish to zero. Rather, there is an optimal amount of squeezing, at which point the minimum phase uncertainty goes as , which is close to the Heisenberg limit. See <refbase>184</refbase>
Yurke state input.
The Heisenberg limit can also be reached using the Mach-Zehnder interferometer by replacing the input light states with this unusual squeezed state
This is known as the Yurke state. It happens to be balanced already, and thus instead of operating our interferometer at , we operate it at , such that the output measurement gives , and , and the final uncertainty in the phase measurement is
For the Yurke state,
In calculating , the terms with drop out, leaving us with
Similarly, it is straightforward to show that
Thus, the uncertainty in is
which is the Heisenberg limit.
Yurke state: Experiment?
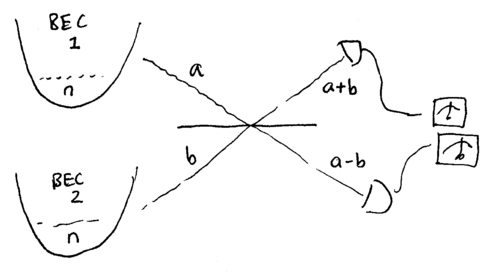
Given how useful the Yurke state could be for interferometry, it is meaningful to consider how such a state might be made. One interesting proposal starts with two Bose-Einstien condenstates, prepared in a state of definite atom number, which we may model as two number eigenstates . The two condensates are weakly linked through a tunnel, which we may model as a beamsplitter, and detectors are placed to look for a single atom at the outputs. This is sketched below:
If the top detector clicks, then one atom has left the condensates; however, it is unknown from which it came. The post-measurement state, after this single click, is thus
written unnormalized. Normalized, the proper post-measurement state is
This is the Yurke state. If the bottom detector had clicked instead, we would have obtained instead, which is also useful.
Similar techniques, involving beamsplitter mixed detection of spontaneous emission, can be used to entangle atoms (as we shall see later). More about this BEC entanglement method can be found in the literature; see, for example, <refbase>185</refbase> , for the proposal to create Yurke states; <refbase>186</refbase>, for an experiment in which a squeezed BEC state was generated, and <refbase>187</refbase>, for a proposal to do Heisenberg limited spectroscopy with BECs.














![{\displaystyle |\psi _{in}\rangle ={\frac {1}{\sqrt {2}}}\left[{|n-1{\rangle }|n\rangle +|n{\rangle }|n-1\rangle }\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fddaf8eca4a41d65a799f1448a487eafc95e3022)